Cho đoạn mạch điện xoay chiều AB không phân nhánh theo thứ tự gồm : đoạn AM chứa biến trở
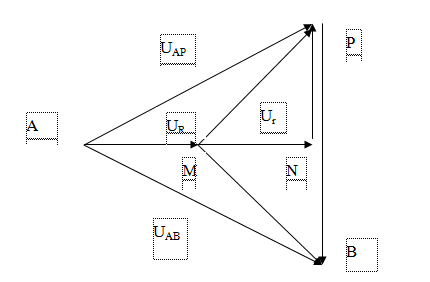
Cho đoạn mạch điện xoay chiều AB không phân nhánh theo thứ tự gồm : đoạn AM chứa biến trở R, đoạn MN chứa điện trở r, đoạn NP chứa cuộn cảm thuần, đoạn PB chứa tụ điện có điện dung C có thể thay đổi được . Đặt vào hai đầu A, B một điện áp u = U0cosωt ( V) ( với U0 và ω không đổi). Ban đầu thay đổi điện dung C đến giá trị C = C0 thì UAP không phụ thuộc vào giá trị của biến trở R. Giữ nguyên giá trị điện dung C0 của tụ điện và thay đổi biến trở thì:
Khi uAP lệch pha cực đại so với uAB thì UPB = U1. Khi ( UAN.UNP) cực đại thì UAM= U2.Biết \({U_{{1_{}}}} = \frac{{25}}{3}{U_2}\)
. Độ lệch pha cực đại giữa uAP và uAB gần nhất với giá trị nào sau đây?
Đáp án đúng là: B
Quảng cáo
Sử dụng định luật Ôm và các biến đổi toán học
khi thay đổi C để UAP không phụ thuộc biến trở R. Dễ có ZC = 2ZL
+ Khi R thay đổi ta luôn có ΔAPB luôn là tam giác cân tại A (Hình vẽ)
Ta thấy khi R thay đổi, nếu ta di chuyển điểm A→M thì góc 2φ chính là độ lệch pha của UAP và UAB càng lớn. Vậy độ lệch pha cực đại của UAP và UAB khi điểm A trùng với điểm M hay lúc đó R=0.
Khi đó:
\({U_1} = {U_{PB}} = \frac{U}{{{Z_1}}}.{Z_C} = \frac{U}{{\sqrt {{r^2} + Z_L^2} }}.2{Z_L}\)
+ Khi R=R0 :
\({U_{AN}}.{U_{NP}} \le \frac{{U_{AN}^2 + U_{NP}^2}}{2} = \frac{{{U^2}}}{2}\)
Vậy UAN.UNP lớn nhất khi UAN=UNP hay khi đó tam giác APB là tam giác vuông cân
Lúc này:
\({U_2} = {U_{AM}} = \frac{U}{{\sqrt 2 }} - {U_r}\)
Từ hình vẽ ta suy ra ZL= R+r; \({Z_2} = \sqrt 2 .(R + r)\)
Nên :
\(\begin{array}{l}
{U_2} = \frac{U}{{\sqrt 2 }} - I.r = \frac{U}{{\sqrt 2 }} - \frac{U}{{{Z_2}}}.r = \frac{U}{{\sqrt 2 }} - \frac{U}{{\sqrt 2 .(R + r)}}.r = \frac{{U.R}}{{\sqrt 2 .(R + r)}}\\
= > {U_2} = \frac{{U.({Z_L} - r)}}{{\sqrt 2 .{Z_L}}}
\end{array}\)
Lại có. Từ đề bài:
\({U_1} = \frac{{25}}{3}.{U_2}\)
Nên ta có:
\(\begin{array}{l}
\frac{U}{{\sqrt {{r^2} + Z_L^2} }}.2.{Z_L} = \frac{{25}}{3}.\frac{{U.({Z_L} - r)}}{{\sqrt 2 .{Z_L}}}\\
= > \frac{{{Z_L}}}{{\sqrt {{r^2} + Z_L^2} }} = \frac{{25}}{{6\sqrt 2 }}.\frac{{{Z_L} - r}}{{{Z_L}}}\\
Z_L^2 = \frac{{25}}{{6\sqrt 2 }}.({Z_L} - r).\sqrt {{r^2} + Z_L^2} \\
{\left( {\frac{{{Z_L}}}{r}} \right)^2} = \frac{{25}}{{6\sqrt 2 }}.\left( {\frac{{{Z_L}}}{r} - 1} \right).\sqrt {1 + {{\left( {\frac{{{Z_L}}}{r}} \right)}^2}}
\end{array}\)
Đặt x=tanφ= ta có PT:
\(\begin{array}{l}
{x^2} = \frac{{25}}{{6\sqrt 2 }}.(x - 1).\sqrt {{x^2} + 1} \\
x \approx 0,8226 = > \varphi = 39,{44^0}\\
2\varphi = {79^0} = \frac{{3\pi }}{7}
\end{array}\)
Đáp án cần chọn là: B
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
