Một vân động viên hàng ngày đạp xe trên đoạn đường thẳng từ điểm A đúng lúc còi báo

Câu hỏi số 261167:

Vận dụng

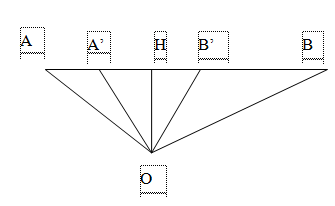
Một vân động viên hàng ngày đạp xe trên đoạn đường thẳng từ điểm A đúng lúc còi báo thức bắt đầu kêu, khi đến điểm B thì còi vừa dứt. Mức cường độ âm tại A và B lần lượt là 60dB và 54 dB. Còi đặt tại điểm O phát âm đẳng hướng với công suất không đổi và môi trường không hấp thụ âm; Cho góc AOB bằng 120⁰. Do vận động viên này khiếm thính nên chỉ nghe được mức cường độ âm từ 61,94 dB trở lên và tốc độ đạp xe không đổi. Biết thời gian còi báo thức kêu là 120s. Trên đoạn đường AB vận động viên nghe thấy tiếng còi báo thức trong khoảng thời gian xấp xỉ bằng

A. 42,67s

B. 41,71s

C. 43,18s

D. 44,15s.

Đáp án đúng là: B

Quảng cáo

Xem lời giải

Câu hỏi:261167

Phương pháp giải

sử dụng các biến đổi toán học về giải tam giác và công thức tính mức cường độ âm.

Giải chi tiết

Ta có hình vẽ sau:

Theo đề bài, mức cường độ âm tại A là 60dB và tại B là 54dB, nên ta có:

\(\begin{array}{l}
{I_A} = {I_0}{.10^6} = {10^{ - 6}}{\rm{W}}/{m^2}\\
{I_B} = {I_0}{.10^{5,4}} = {251.10^{ - 9}}{\rm{W}}/{m^2}\\
\frac{{{I_A}}}{{{I_B}}} = \frac{{{r_b}^2}}{{{r_a}^2}} = \frac{{{{10}^{ - 6}}}}{{{{251.10}^{ - 9}}}} \approx 4 = > \frac{{{r_b}}}{{{r_a}}} \approx 2
\end{array}\)

Áp dụng hệ thức lượng trong tam giác OAB ta có:

\(\begin{array}{l}
A{B^2} = A{O^2} + O{B^2} - 2OA.OB.\cos {120^0}\\
A{B^2} = r_a^2 + 4r_a^2 + 2{r_{2.}}.2{r_a}.\frac{1}{2} = 7r_a^2\\
= > AB = \sqrt 7 {r_a}
\end{array}\)

Tai người này chỉ nghe được âm thanh có mức cường độ âm lớn hơn 61,94dB, ta gọi đoạn đường mà người đó nghe được tiếng còi là từ A’ đến B’. A’ và B’ đối xứng nhau qua H là đường cao của tam giác OAB. (tại H âm nghe được có mức cường độ âm lớn nhất vì H gần O nhất).

Cường độ âm tại A’ là:

\(\begin{array}{l}
{I_{A'}} = {I_0}{.10^{6,194}} = {1563.10^{ - 9}}{\rm{W}}/{m^2}\\
\frac{{{I_{A'}}}}{{{I_A}}} = \frac{{{r_a}^2}}{{{r_{a'}}^2}} = \frac{{{{1563.10}^{ - 9}}}}{{{{10}^{ - 6}}}} \approx \frac{1}{{0,64}} = > {r_{a'}} = 0,8{r_a}
\end{array}\)

Độ dài đoạn OH được xác định thông qua công thức tính diện tích tam giác OAB như sau:

\(\begin{array}{l}

{S_{AOB}} = \frac{1}{2}OH.AB = \frac{1}{2}OA.OB.sin{120^0}\\
= > OH = \frac{{OA.OB.sin{{120}^0}}}{{AB}} = \frac{{{r_a}.2{r_a}.\frac{{\sqrt 3 }}{2}}}{{\sqrt 7 {r_a}}} = \frac{3}{{\sqrt {21} }}{r_a} = \frac{{\sqrt {21} }}{7}.{r_a}\\
= > A'H = \sqrt {A'{O^2} - O{H^2}} \approx 0,46{r_a}\\
= > A'B' = 2A'H \approx 0,92{r_a}
\end{array}\)

Thời gian mà người đo nghe thấy còi chính là thời gian đi đoạn A’B’ :

\(\Delta t = \frac{{A'B'}}{v} = \frac{{0,92{r_a}}}{{\frac{{AB}}{{120}}}} = \frac{{0,92{r_a}}}{{\sqrt 7 {r_a}}}.120 = 41,71s\)

Đáp án cần chọn là: B

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.