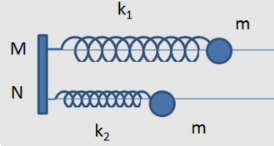
Cho hai con lắc lò xo nằm ngang (k1, m) và (k2, m) như hình vẽ. Trục dao động M và N cách nhau 9cm.

Câu hỏi số 332871:

Vận dụng cao

Cho hai con lắc lò xo nằm ngang (k₁, m) và (k₂, m) như hình vẽ. Trục dao động M và N cách nhau 9cm. Lò xo k₁ có độ cứng 100 N/m ; chiều dài tự nhiên l₁= 35cm. Lò xo k₂có độ cứng 25N/m, chiều dài tự nhiên l₂ = 26cm. Hai vật có khối lượng cùng bằng m. Thời điểm ban đầu (t = 0), giữ lò xo k₁ dãn một đoạn 3cm, lò xo k₂ nén một đoạn 6cm rồi đồng thời thả nhẹ để hai vật dao động điều hoà. Bỏ qua mọi ma sát. Khoảng cách nhỏ nhất giữa hai vật trong quá trình dao động xấp xỉ bằng :

A. 11cm

B. 10cm

C. 9cm

D. 13cm

Đáp án đúng là: B

Quảng cáo

Xem lời giải

Câu hỏi:332871

Phương pháp giải

Phương pháp :

Viết phương trình dao động của hai vật : x₁; x₂

Khoảng cách giữa hai vật theo phương ngang : \(\Delta x = \left| {{x_1} - {x_2}} \right|\) → Khoảng cách nhỏ nhất giữa hai vật theo phương ngang trong quá trình dao động là : ∆x_min.

Khoảng cách nhỏ nhất giữa hai vật trong quá trình dao động là : \({d_{\min }} = \sqrt {M{N^2} + \Delta x_{\min }^2} \)

Giải chi tiết

Cách giải :

- Tần số góc của vật 1 và vật 2 là : \(\left\{ \begin{array}{l}{\omega _1} = \sqrt {\frac{{{k_1}}}{m}} = \sqrt {\frac{{100}}{m}} = \frac{{10}}{{\sqrt m }}\\{\omega _2} = \sqrt {\frac{{{k_2}}}{m}} = \sqrt {\frac{{25}}{m}} = \frac{5}{{\sqrt m }}\end{array} \right. \Rightarrow {\omega _1} = 2{\omega _2}\)

- Lò xo k₁ có chiều dài tự nhiên l₁= 35cm. Lò xo k₂có chiều dài tự nhiên l₂ = 26cm → Vị trí cân bằng của hai lò xo cách nhau theo phương ngang 1 đoạn : 35 – 26 = 9cm

- Thời điểm ban đầu (t = 0), giữ lò xo k₁ dãn một đoạn 3cm, lò xo k₂ nén một đoạn 6cm rồi đồng thời thả nhẹ để hai vật dao động điều hoà. Chọn gốc toạ độ trùng với VTCB của lò xo k₁.

→ Phương trình dao động điều hoà của hai vật : \(\left\{ \begin{array}{l}{x_1} = 3\cos \left( {{\omega _1}t} \right) = 3\cos \left( {2.{\omega _2}t} \right)\\{x_2} = - 9 + 6\cos \left( {{\omega _2}t + \pi } \right) = - 9 - 6\cos \left( {{\omega _2}t} \right)\end{array} \right.\)

→ Khoảng cách giữa hai vật theo phương ngang trong quá trình dao động là :

\(\Delta x = \left| {{x_1} - {x_2}} \right| = \left| {3\cos \left( {2.{\omega _2}t} \right) + 9 + 6\cos \left( {{\omega _2}t} \right)} \right|\)

Vì :

\(\begin{array}{l}\cos \left( {2.{\omega _2}t} \right) = 2{\cos ^2}\left( {{\omega _2}t} \right) - 1 \Rightarrow \Delta x = \left| {3\left( {2{{\cos }^2}\left( {{\omega _2}t} \right) - 1} \right) + 9 + 6\cos \left( {{\omega _2}t} \right)} \right|\\ \Rightarrow \Delta x = \left| {6.{{\cos }^2}\left( {{\omega _2}t} \right) + 6\cos \left( {{\omega _2}t} \right) + 6} \right|\end{array}\)

Đặt : \(a = \cos \left( {{\omega _2}t} \right) \Rightarrow \Delta x = \left| {6.{a^2} + 6a + 6} \right|\)

Ta có :

\(\begin{array}{l}6.{a^2} + 6a + 6 = 6\left( {{a^2} + a + 1} \right) = 6\left( {{{\left( {a + \frac{1}{2}} \right)}^2} + \frac{3}{4}} \right) = 6.{\left( {a + \frac{1}{2}} \right)^2} + 4,5\\6.{\left( {a + \frac{1}{2}} \right)^2} + 4,5 \le 4,5 \Rightarrow {\left( {6.{a^2} + 6a + 6} \right)_{\min }} = 4,5\\ \Rightarrow \Delta {x_{\min }} = 4,5cm\end{array}\)

→ Khoảng cách nhỏ nhất giữa hai vật trong quá trình dao động là :

\({d_{\min }} = \sqrt {M{N^2} + \Delta x_{\min }^2} = \sqrt {{9^2} + 4,{5^2}} = 10,06cm\)

Đáp án cần chọn là: B

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.