Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 1 - Ngày 20-21/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Môn Toán

Cho hình

Cho hình vẽ

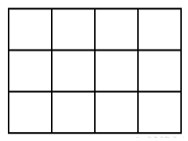
Trả lời cho các câu 1, 2 dưới đây:

Câu hỏi số 1:
Vận dụng

Có bao nhiêu hình chữ nhật trong hình vẽ. 

Đáp án đúng là: C

Xem lời giải
Câu hỏi:391904
Phương pháp giải

Cách 1: Suy luận, trên hình vẽ có 4 đường thẳng song song nằm ngang và 5 đường thẳng song song thẳng đứng. Ta thấy cứ một cặp đường thẳng song song nằm ngang và một cặp đường thẳng song song thẳng đứng thì tạo thành một hình chữ nhật.

Nhận xét:

4 đường thẳng nằm ngang tạo thành:

\(\frac{{4 \times \left( {4 - 1} \right)}}{2} = 6\) (cặp đường thẳng nằm ngang)

5 đường thẳng đứng tạo thành:

\(\frac{{5 \times 4}}{2} = 10\) (cặp đường hẳng đứng)

Từ đó, lập luận tiếp để tìm ra số hình chữ nhật.

Cách 2: Nhận xét: Mỗi giao điểm đều là đỉnh của 12 hình chữ nhật.

Có \(4 \times 5 = 20\) (giao điểm), chúng là đỉnh của:

\(20 \times 12 = 240\) (hình chữ nhật)

Nhưng làm như vậy mỗi hình chữ nhật đều được tính 4 lần (ở 4 đỉnh) nên thực ra chỉ có:

Từ đó tính được số hình chữ nhật thực tế.

Giải chi tiết

Cách 1: Trên hình vẽ có 4 đường thẳng song song nằm ngang và 5 đường thẳng song song thẳng đứng. Ta thấy cứ một cặp đường thẳng song song nằm ngang và một cặp đường thẳng song song thẳng đứng thì tạo thành một hình chữ nhật.

Nhận xét:

4 đường thẳng nằm ngang tạo thành:

\(\frac{{4 \times \left( {4 - 1} \right)}}{2} = 6\) (cặp đường thẳng nằm ngang)

5 đường thẳng đứng tạo thành:

\(\frac{{5 \times 4}}{2} = 10\) (cặp đường hẳng đứng)

Ta thấy:

6 cặp đường thẳng nằm ngang tạo thành với 1 cặp đường thẳng đứng 6 hình chữ nhật.

Vậy 6 cặp đường thẳng nàm ngang tạo thành với 10 cặp đường thẳng đứng: \(6 \times 10 = 60\) (hình chữ nhật)

Đáp số: 60 hình chữ nhật.

Cách 2: Nhận xét: Mỗi giao điểm đều là đỉnh của 12 hình chữ nhật.

Có \(4 \times 5 = 20\) (giao điểm), chúng là đỉnh của:

\(20 \times 12 = 240\) (hình chữ nhật)

Nhưng làm như vậy mỗi hình chữ nhật đều được tính 4 lần (ở 4 đỉnh) nên thực ra chỉ có:

\(240:4 = 60\) (hình chữ nhật)

Đáp số: 60 hình chữ nhật.

 

Đáp án cần chọn là: C

Câu hỏi số 2:
Vận dụng

Biết cạnh của các ô vuông trong hình vẽ đều dài 1cm, hãy tính tổng chu vi và tổng diện tích của tất cả các hình vuông có trong hình vẽ.

Đáp án đúng là: A

Xem lời giải
Câu hỏi:391905
Phương pháp giải

Áp dụng công thức tính chu vi và diện tích hình vuông.

Giải chi tiết

Có 12 hình vuông có cạnh 1cm.

Có 6 hình vuông có cạnh 2cm.

Có 2 hình vuông có cạnh 3cm.

Tổng chu vi các hình vuông là:

\(\left( {1 \times 4} \right) \times 12 + \left( {2 \times 4} \right) \times 6 + \left( {3 \times 4} \right) \times 2 = 120\left( {cm} \right)\)

Tổng diện tích các hình vuông là:

\(\left( {1 \times 1} \right) \times 12 + \left( {2 \times 2} \right) \times 6 + \left( {3 \times 3} \right) \times 2 = 54\left( {c{m^2}} \right)\)

Đáp số:  120cm và \(54c{m^2}.\)

Đáp án cần chọn là: A

Quảng cáo

Tham Gia Group Dành Cho 2K14 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến các môn Toán, Tiếng Việt, Tiếng Anh lớp 5 trên Tuyensinh247.com. Cam kết giúp con lớp 5 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn