Bến xe A và B nằm ở các đỉnh của một hình vuông có chiều dài cạnh L = 120 km (Hình 1). Có hai

Câu hỏi số 677215:

Vận dụng cao

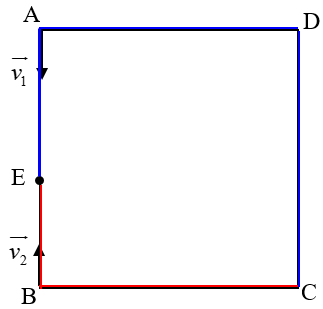
Bến xe A và B nằm ở các đỉnh của một hình vuông có chiều dài cạnh L = 120 km (Hình 1). Có hai cách để di chuyển từ A đến B: đi thẳng từ A đến B, hoặc đi dọc theo ba cạnh còn lại của hình vuông. Hàng ngày, hai xe buýt chạy trên đoạn đường thẳng từ A đến B và từ B đến A, chúng khởi hành cùng lúc và đi về phía nhau. Một hôm, hai xe buýt gặp nhau đúng chỗ một cây lớn đổ xuống ngang đường nên các lái xe quyết định quay đầu và cho xe đi theo đường vòng qua các cạnh còn lại của hình vuông. Hỏi cây đổ ở cách bến xe A bao xa để hai xe buýt có thể gặp nhau ở đỉnh C? Giả sử rằng tốc độ xe buýt không đổi.

Quảng cáo

Xem lời giải

Câu hỏi:677215

Phương pháp giải

Quãng đường trong chuyển động thẳng đều: s = v.t

Hai xe gặp nhau khi thời gina chuyển động bằng nhau.

Giải chi tiết

Giả sử vị trí cây đổ ở điểm E

Ban đầu hai xe gặp nhau tại E, ta có:

\(\dfrac{{AE}}{{{v_1}}} = \dfrac{{BE}}{{{v_2}}} \Rightarrow \dfrac{{AE}}{{{v_1}}} = \dfrac{{BE}}{{{v_2}}}\,\,\left( 1 \right)\)

Sau đó hai xe từ E quay trở lại và gặp nhau tại C, ta có:

\(\begin{array}{l}\dfrac{{EA + AD + DC}}{{{v_1}}} = \dfrac{{EB + BC}}{{{v_2}}}\\ \Rightarrow \dfrac{{EA}}{{{v_1}}} + \dfrac{{240}}{{{v_1}}} = \dfrac{{EB}}{{{v_2}}} + \dfrac{{120}}{{{v_2}}}\,\,\left( 2 \right)\end{array}\)

Trừ hai vế phương trình (2) và (1) ta có:

\(\dfrac{{240}}{{{v_1}}} = \dfrac{{120}}{{{v_2}}} \Rightarrow {v_1} = 2{v_2}\)

Thay vào (1) ta có:

\(\begin{array}{l}\dfrac{{AE}}{{2{v_2}}} = \dfrac{{120 - AE}}{{{v_2}}} \Rightarrow \dfrac{{AE}}{2} = 120 - AE\\ \Rightarrow \dfrac{3}{2}AE = 120 \Rightarrow AE = 80\,\,\left( {km} \right)\end{array}\)

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link