Một người bán buôn Thanh Long Đỏ nhận thấy rằng: Nếu bán với giá 20000 đồng/kg thì mỗi

Câu hỏi số 733189:

Vận dụng

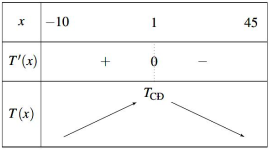
Một người bán buôn Thanh Long Đỏ nhận thấy rằng: Nếu bán với giá 20000 đồng/kg thì mỗi tuần có 90 khách đến mua và mỗi khách mua trung bình 60 kg. Cứ tăng giá 2000 đồng/kg thì số khách mua hàng tuần giảm đi 1 và khi đó mỗi khách lại mua ít hơn mức trung bình 5 kg , và như vậy cứ giảm giá 2000 đồng/kg thì số khách mua hàng tuần tăng thêm 1 và khi đó mỗi khách lại mua nhiều hơn mức trung bình 5 kg. Hỏi người đó phải bán với giá mỗi kg là bao nhiêu để lợi nhuận thu được hàng tuần là lớn nhất, biết rằng người đó phải nộp tổng các loại thuế là 2200 đồng/kg (kết quả làm tròn đến hàng nghìn).

A. 16000đ .

B. 12000đ.

C. 24000đ.

D. 22000đ.

Đáp án đúng là: D

Quảng cáo

Xem lời giải

Câu hỏi:733189

Giải chi tiết

Giả sử giá bán thay đổi $x$ lần, mỗi lần thay đổi 2000 đồng $(x \in \mathbb{Z}, x>0$ là tăng giá, $x<0$ là giảm giá).

Theo thực tế thì $-10<x<45$ (giá bán trên 0 đồng và còn ít nhất một khách).

Tổng tiển thu được sau khi thay đổi là

$T=(90-x)(60-5 x)(20+2 x-2,2)=10 x^3-931 x^2+1772 x+96120$

Xét hàm số $T(x)=10 x^3-931 x^2+1772 x+96120$ .

Bài toán trở thành tìm GTLN của $T(x)$ với $x \geq 20000$ .

Ta có $T^{\prime}(x)=30\left(x^2-62,0667 x+57,4\right)$ .

$T^{\prime}=0 \Leftrightarrow \left[\begin{array}{l} x \approx 1 \\ x \approx 61 \end{array}\right.$

Bảng biến thiên của $T(x)$ :

Vậy giá bán đưa ra để lợi nhuận cao nhất là 22 000.

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.