Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 2 - Ngày 27-28/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn Hóa

Một hệ gồm nAO (n =2; 3; …) của cùng một nguyên tử, có thể tổ hợp với nhau để tạo ra hệ

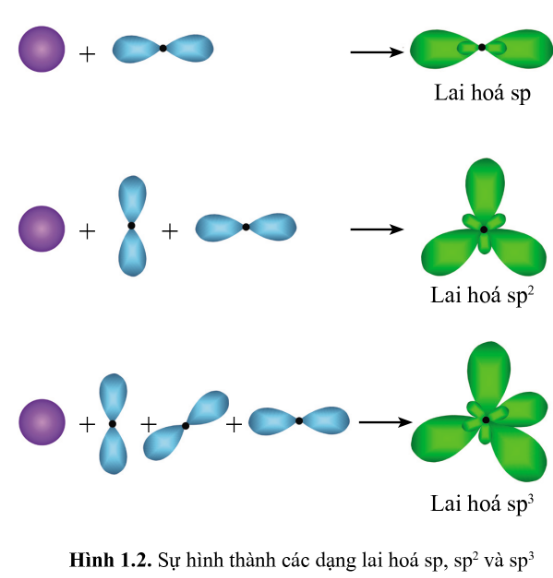
Một hệ gồm nAO (n =2; 3; …) của cùng một nguyên tử, có thể tổ hợp với nhau để tạo ra hệ n orbital mới (gọi là orbital lai hoá) có hình dạng như nhau, nhưng có định hướng không gian phù hợp với sự hình thành liên kết và dạng hình học phân tử tương ứng. Lai hoá là sụ tổ hợp các orbital của cùng nguyên tư để tạo ra các orbital mó́i có cùng dạng hình học và năng luợng nhưng có định huớng khác nhau trong không gian. Sự lai hoá thường chỉ xét với nguyên tử trung tâm.

Trả lời cho các câu 1, 2, 3, 4 dưới đây:

Câu hỏi số 1:
Nhận biết

Lai hoá là sự tổ hợp các orbital thuộc các nguyên tử khác nhau để tạo thành các orbital lai có năng lượng và định hướng giống nhau.

Đáp án đúng là: B

Xem lời giải
Câu hỏi:776681
Phương pháp giải

Khái niệm lai hóa.

Giải chi tiết

Lai hoá là sự tổ hợp các AO (orbital nguyên tử) của cùng một nguyên tử, không phải của các nguyên tử khác nhau. Mục đích là tạo ra các orbital mới có hình dạng và năng lượng tương tự nhau, đồng thời định hướng phù hợp với liên kết.

Đáp án cần chọn là: B

Câu hỏi số 2:
Thông hiểu

Tại sao các orbital cần lai hóa trước khi xen phủ tạo liên kết?

Đáp án đúng là: D

Xem lời giải
Câu hỏi:776682
Phương pháp giải

Hiểu bản chất của lai hoá: tạo điều kiện hình thành liên kết hoá học thuận lợi.

Giải chi tiết

Quá trình lai hoá tạo ra các orbital có hình dạng giống nhau, năng lượng tương đương và định hướng không gian phù hợp, giúp nguyên tử trung tâm hình thành liên kết bền vững và xác định dạng hình học phân tử.

Đáp án cần chọn là: D

Câu hỏi số 3:
Thông hiểu

Cho biết các phát biểu sau về oribital lại hóa đúng hay sai?

Đúng Sai
a) Lai hoá chỉ xảy ra giữa các orbital thuộc nguyên tử trung tâm.
b) Sau khi lai hoá, các orbital mới có năng lượng giống hệt nhau.
c) Các orbital lai hoá có định hướng không gian khác nhau nhưng hình dạng hoàn toàn khác nhau.
d) Số orbital lai hoá tạo thành luôn bằng số orbital tham gia lai hoá ban đầu.

Đáp án đúng là: Đ; Đ; S; Đ

Xem lời giải
Câu hỏi:776683
Phương pháp giải

Ý nghĩa lai hóa orbital.

Giải chi tiết

a) đúng, vì AO lai hóa chỉ xét các AO của nguyên tử trung tâm.

b) đúng, vì sau khi lai hóa, các orbital lai hóa có mức năng lượng giống nhau, hình dạng giống nhau.

c) sai, vì oribital lai hóa có hình dạng tương tự nhau, nhưng hướng khác nhau do đó không hoàn toàn khác nhau.

d) đúng, số lượng orbital lai hóa bảo toàn số lượng trước và sau lai hóa.

Đáp án cần chọn là: Đ; Đ; S; Đ

Câu hỏi số 4:
Vận dụng

Một nguyên tử thực hiện lai hoá giữa 1 orbital s và 2 orbital p để tạo thành 3 orbital lai hoá có cùng hình dạng và định hướng phù hợp trong không gian. Quá trình lai hoá này được gọi là lai hoá_______

Đáp án đúng là: sp2

Xem lời giải
Câu hỏi:776684
Phương pháp giải

Tính số AO tham gia (1s + 2p = 3 AO), từ đó xác định tên loại lai hoá tương ứng.

Giải chi tiết

Lai hoá sp² là sự tổ hợp giữa 1 orbital s và 2 orbital p → tạo ra 3 orbital lai hoá giống nhau về năng lượng và hình dạng, có định hướng tạo thành mặt phẳng tam giác → phù hợp với hình học phân tử tam giác phẳng.

Đáp án cần điền là: sp2

Quảng cáo

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn