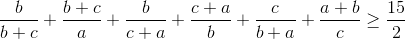Bất đẳng thức - Bất phương trình
Cho a , b , c > 0 . Chứng minh rằng:
Quảng cáo
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com



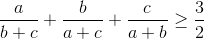 (1)
(1)![\begin{matrix} \frac{b+c}{a}+\frac{a+c}{b}+\frac{b+a}{c}\geq 3\sqrt[3]{\frac{(a+b)(b+c)(c+a)}{abc}}\\ (a+b)(b+c)(c+a)\geq 8abc \end{matrix}](http://images.tuyensinh247.com/picture/learning/exam/2015/0831/v99301_496688_2.gif)
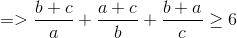 (1)
(1)