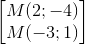Hình giải tích phẳng
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng (∆):x+y+2=0 và đường tròn (C):x2+y2-4x-2y=0. Gọi I là tâm của đường tròn (C), M là điểm thuộc (∆). Qua M kẻ các tiếp tuyến MA, MB đến (C) (A,B là các tiếp điểm). Tìm tọa độ điểm M, biết tứ giác MAIB có diện tích bằng 10
Đáp án đúng là: A
Quảng cáo
Đáp án cần chọn là: A
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com



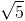
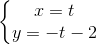 , (t∈R) =>M(t;-t-2)
, (t∈R) =>M(t;-t-2)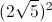 +
+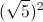 =25
=25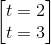 =>
=>