Tại một vị trí trên bờ, bạn An có thể xác định được khoảng cách hai chiếc thuyền ở vị

Câu hỏi số 209766:

Vận dụng

Tại một vị trí trên bờ, bạn An có thể xác định được khoảng cách hai chiếc thuyền ở vị trí A, vị trí B bằng cách như sau: Trước tiên, bạn chọn một vị trí trên bờ ( điểm I) sao cho ba điểm I, A, B thẳng hàng. Sau đó, bạn di chuyển theo hướng vuông góc với IA đến vị trí điểm K cách điểm I khoảng \(380m\). Bạn dùng giác kế nhắm vị trí điểm A, điểm B thì đo được góc \({{15}^{0}}\). Còn khi bạn nhắm vị trí điểm A, điểm I thì đo được góc \({{50}^{0}}\). Hỏi khoảng cách hai chiếc thuyền là bao nhiêu?

A. \(362m\)

B. \(256m\)

C. \(200m\)

D. \(300m\)

Đáp án đúng là: A

Quảng cáo

Xem lời giải

Câu hỏi:209766

Phương pháp giải

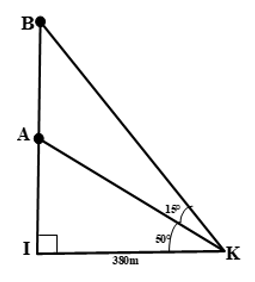
Phân tích bài toán:

Đây là một bài tập theo đúng nghĩa là ứng dụng thực tế. Một bài tập về dùng giác kế để đo góc, rồi dùng các tỉ số lượng giác trong tam giác vuông để tính ra khoảng cách giữa các vật. Phương pháp đo này dùng để đo những đối tượng thường là bị ngăn cách mà ta không thể sử dụng thước để đo trực tiếp được, ví dụ: đo khoảng cách giữa hai ngọn núi, khoảng cách giữa hai chiếc thuyền trên biển hay đo chiều cao của một cái cây chẳng hạn. Khi giải bài tập loại này các em chỉ cần sử dụng tỉ số lượng giác trong tam giác vuông là làm được.

Giải chi tiết

Do KA nằm giữa KI và KB nên:

\(\widehat{BKI}=\widehat{BKA}+\widehat{AKI}={{15}^{0}}+{{50}^{0}}={{65}^{0}}\). Xét tam giác vuông AKI, vuông tại I, ta có: \(\tan AKI=\dfrac{AI}{IK}\Rightarrow AI=IK.\tan AKI=380.\tan {{50}^{0}}\) (mét) Xét tam giác vuông BKI, vuông tại I, ta có: \(\tan BKI=\dfrac{BI}{IK}\Rightarrow BI=IK.\tan BKI=380.\tan {{65}^{0}}\) (mét) Khoảng cách hai chiếc thuyền chính là độ dài đoạn AB:

\(AB=BI-AI=380.\tan{{65}^{0}}-380.\text{ }\tan{{50}^{0}}=380.\left( \tan{{65}^{0}}-\tan{{50}^{0}} \right)=362\) (mét)

Đáp án cần chọn là: A

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link