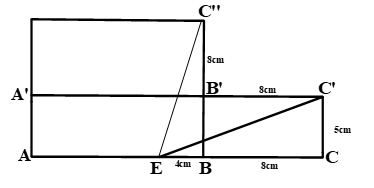
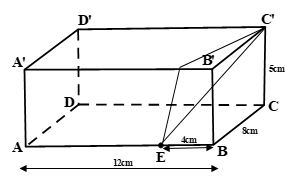
Một chiếc hộp hình hộp chữ nhật \(ABCD.ABCD\) có \(AB=12cm,BC=8cm,BB=5cm\), điểm \(E\) thuộc
Một chiếc hộp hình hộp chữ nhật \(ABCD.ABCD\) có \(AB=12cm,BC=8cm,BB=5cm\), điểm \(E\) thuộc cạnh \(AB\) và \(EB=4cm\) . Chiếc hộp được đặt trên sàn. Một con kiến bò trên mặt chiếc hộp từ \(E\) đến \(C'\). Tính độ dài đoạn đường đi ngắn nhất của con kiến.
Đáp án đúng là: D
Quảng cáo
Phân tích bài toán:
Đây là một bài hình không gian, mang tính phân loại học sinh. Bài toán này đòi hỏi học sinh phải có khả năng tư duy tốt, biết chuyển đổi từ một hình không gian về một hình học phẳng. Có một số em hiểu sai đề bài và cho rằng con kiến sẽ đi theo các “mép” cạnh để tới điểm C’ nên cộng tổng độ dài các cạnh lại. Thực tế con kiến đi trên bề mặt của chiếc hộp chứ không phải bò trên các “mép” cạnh. Để dễ hiểu hơn các em cứ tượng tưởng mình có một chiếc hộp như trên. Sau đó, mình tháo ra và duỗi phẳng chiếc hộp để ra điểm C’’( thực ra là điểm C’, ghi như vậy để phân biệt) hoặc tháo hai bên “hông” của hộp để ra điểm C’. Rồi ta áp dụng định lý pitago để tính.
Điểm C’’ cũng chính là điểm C’ Con kiến có hai cách bò từ E đên C’
Cách 1: Vượt qua cạnh BB’
Đoạn đường đi ngắn nhất trong trường hợp này là
\(EC'=\sqrt{{{\left( EB+BC \right)}^{2}}+CC{{'}^{2}}}=\sqrt{{{\left( 4+8 \right)}^{2}}+{{5}^{2}}}=13cm\)
Cách 2: Vượt qua cạnh A’B’
Đoạn đường đi ngắn nhất trong trường hợp này là
\(EC' = \sqrt {{{\left( {BB' + B'C''} \right)}^2} + E{B^2}} = \sqrt {{{\left( {5 + 8} \right)}^2} + {4^2}} = \sqrt {185} cm\)
So sánh hai cách bò trên, đoạn đường đi ngắn nhất của con kiến là \(13cm\)
(Không xét con đường mà con kiến bò vượt qua cạnh AA’, vì con đường này rõ ràng dài hơn các con đường trên).
Đáp án cần chọn là: D
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
