Trên cùng một đường thẳng đứng, người ta ném đồng thời hai vật theo phương ngang. Vật A ở

Câu hỏi số 286106:

Vận dụng

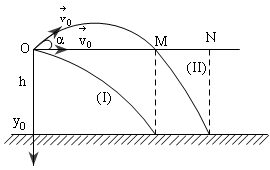
Trên cùng một đường thẳng đứng, người ta ném đồng thời hai vật theo phương ngang. Vật A ở độ cao h₁, vật B độ cao h₂ (so với sàn nằm ngang) với các vận tốc ban đầu tương ứng là v₀₁ và v₀₂. Bỏ qua mọi lực cản. Lấy g=10m/s².

a. Cho h₁=80m và v₀₁=10m/s. Viết phương trình quỹ đạo của vật A. Tìm khoảng cách từ vị trí ném vật A đến điểm mà vật A chạm sàn lần đầu tiên.

b. Vật B va chạm đàn hồi với sàn (vận tốc tuân theo quy luật phản xạ gương), nẩy lên và rơi xuống sàn lần thứ hai cùng một vị trí và cùng thời điểm với vật A chạm sàn lần đầu tiên. Tìm tỉ số \(\frac{{{v}_{01}}}{{{v}_{02}}}\)và \(\frac{{{h}_{1}}}{{{h}_{2}}}\).

Quảng cáo

Xem lời giải

Câu hỏi:286106

Phương pháp giải

Khảo sát chuyển động của một vật ném ngang

Giải chi tiết

a. Chọn hệ trục Oxy như hình vẽ, gốc O trùng với vị trí ban đầu của vật A, trục Oy thẳng đứng hướng xuống dưới.

Phương trình quỹ đạo của vật A: \({{y}_{1}}=\frac{g}{2.v_{01}^{2}}.x_{1}^{2}\) =>\({{y}_{1}}=\frac{x_{1}^{2}}{20}\left( m \right)\)

Khoảng thời gian từ lúc vật A chuyển động đến thời điểm vật A chạm sàn lần đầu: \({{y}_{1}}=\frac{g}{2}{{t}^{2}}\) => \({{t}_{1}}=\sqrt{\frac{2{{h}_{1}}}{g}}=4s\)

Khoảng cách từ vị trí ném vật A đến điểm mà vật A chạm sàn lần đầu tiên: \({{x}_{1}}={{v}_{01}}.t\) => \(L=10.4=40m\)

b. Thời gian vật B va chạm sàn lần đầu: \({{t}_{2}}=\sqrt{\frac{2{{h}_{2}}}{g}}\)

Vị trí vật 2 chạm sàn lần 1: x_2C= v₀₂. \(\sqrt{\frac{2{{h}_{2}}}{g}}\)

Vận tốc của vật B khi va chạm với sàn lần thứ nhất : v_x = v_01;v_y = g.t₂ =\(\sqrt{2g{{h}_{2}}}\)

Sau khi va chạm lần thứ nhất tại C, vì vận tốc tuân theo quy luật phản xạ gương nên tại C vật tiếp tục chuyển động ném xiên với các thành phần vận tốc v_{xc =}= v₀₁và v_yc= -\(\sqrt{2g{{h}_{2}}}\) có hướng như hình vẽ.

Phương trình chuyển động vật 2 sau khi va chạm lần thứ nhất: x₂ = x_2c + v_xc.t^’

\(\begin{array}{l}
{y_2} = {v_{yC}}.t' + \frac{{gt{'^2}}}{2}\\
= > {y_2} = - \sqrt {2g{h_2}} t' + \frac{{gt{'^2}}}{2}
\end{array}\)

(t^’ là khoảng thời gian vật chuyển động từ thời điểm ở điểm C)

Vị trí vật B chạm sàn lần 2:\({{x}_{2}}=\) v₀₂. \(\sqrt{\frac{2{{h}_{2}}}{g}}\)+ v₀₂.\(\left( \sqrt{\frac{2{{h}_{1}}}{g}}-\sqrt{\frac{2{{h}_{2}}}{g}} \right)\)

Theo giả thiết: \({{x}_{2}}={{x}_{1}}={{v}_{01}}.\sqrt{\frac{2{{h}_{1}}}{g}}\)

v₀₂. \(\sqrt{\frac{2{{h}_{2}}}{g}}\)+ v₀₂. \(\left( \sqrt{\frac{2{{h}_{1}}}{g}}-\sqrt{\frac{2{{h}_{2}}}{g}} \right)\) = \({{v}_{01}}.\sqrt{\frac{2{{h}_{1}}}{g}}\)=> v₀₂= v₀₁hay \(\frac{{{v}_{01}}}{{{v}_{02}}}=1\)

\(\begin{array}{l}
{y_2} = - \sqrt {2g{h_2}} \left( {\sqrt {\frac{{2{h_1}}}{g}} - \sqrt {\frac{{2{h_2}}}{g}} } \right) + \frac{g}{2}{\left( {\sqrt {\frac{{2{h_1}}}{g}} - \sqrt {\frac{{2{h_2}}}{g}} } \right)^2} = 0\\
= > - 2\sqrt {{h_2}{h_1}} + 2{h_2} + {h_1} + {h_2} - 2\sqrt {{h_2}{h_1}} = 0\\
= > {h_1} - 4\sqrt {{h_2}{h_1}} + 3{h_2} = 0\\
\Delta ' = {\left( {2\sqrt {{h_2}} } \right)^2} - 3{h_2} = {h_2}\\
\Rightarrow \left[ \begin{array}{l}
{h_1} = \sqrt {{h_2}} \\
{h_1} = 3\sqrt {{h_2}}
\end{array} \right.
\end{array}\)

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10