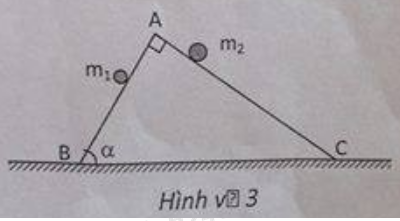
Một nêm có tiết diện là tam giác ABC vuông tại A, và hai bên là AB và AC. Cho hai vật m1 và m2

Câu hỏi số 286110:

Vận dụng cao

Một nêm có tiết diện là tam giác ABC vuông tại A, và hai bên là AB và AC. Cho hai vật m₁ và m₂ chuyển động đồng thời không vận tốc đầu từ A trên hai mặt nêm. Bỏ qua moi ma sát. Lấy g=10m/s² (Hình 4).

a. Giữ nêm cố định, thời gian 2 vật m₁ và m₂ trượt đến các chân mặt nêm AB và AC tương ứng là t₁ và t₂ với t₂ = 2t₁. Tìm \(\alpha \)

b. Để t₁ = t₂ thì cần phải cho nêm chuyển động theo phương ngang một gia tốc a₀ không đổi bẳng bao nhiêu?

Quảng cáo

Xem lời giải

Câu hỏi:286110

Phương pháp giải

Áp dụng định luật II Niu – tơn, chuyển động nhanh dần đều, hệ quy chiếu quán tính.

Giải chi tiết

a. Áp dụng định luật II Niu – tơn vật 1: \(\overrightarrow{{{P}_{1}}}+\overrightarrow{{{N}_{1}}}={{m}_{1}}\overrightarrow{{{a}_{1}}}\)(1)

Chiếu (1) lên hướng chuyển động vật 1: \({{P}_{1}}\sin \alpha ={{m}_{1}}{{a}_{1}}\)=> \(\)=> \({{s}_{1}}=AB=BC\cos \alpha =g\sin \alpha \frac{t_{1}^{2}}{2}\) (*)

Áp dụng định luật II Niu – tơn vật 2: \(\overrightarrow{{{P}_{2}}}+\overrightarrow{{{N}_{2}}}={{m}_{2}}\overrightarrow{{{a}_{2}}}\)(2)

Chiếu (2) lên hướng chuyển động vật 2: \({{P}_{2}}\cos \alpha ={{m}_{2}}{{a}_{2}}\)=> \({{a}_{2}}=g\cos \alpha \)

=> \({{s}_{2}}=AC=BC\sin \alpha =g\cos \alpha \frac{t_{2}^{2}}{2}\) (**)

Từ (*) và (**): \({{\left( \frac{{{t}_{1}}}{{{t}_{2}}} \right)}^{2}}\tan \alpha =\frac{1}{\tan \alpha }\)

Vì t₂ = 2t₁=> \(\tan \alpha =\pm 2\)=> \(\alpha \approx {{63}^{0}}{{26}^{'}}\)

b. Chọn hệ quy chiếu gắn với nêm. Khi đó mỗi vật sẽ chịu tác dụng thêm một lực quán tính hướng sang bên trái.

Gọi \(\overrightarrow{{{a}_{1}}}\), \(\overrightarrow{{{a}_{2}}}\)lần lượt là gia tốc của vật 1, vật 2 so với nêm

Áp dụng định luật II Niu – tơn cho vật 1: \(\overrightarrow{{{P}_{1}}}+\overrightarrow{{{N}_{1}}}+\overrightarrow{{{F}_{qt1}}}={{m}_{1}}\overrightarrow{{{a}_{1}}}\) (3)

Chiếu (3) lên hướng chuyển động vật 1 và lên phương vuông góc hướng lên: \({{P}_{1}}\sin \alpha +{{F}_{qt1}}\cos \alpha ={{m}_{1}}{{a}_{1}}\)

Và \(-{{P}_{1}}\cos \alpha +{{F}_{qt1}}\sin \alpha =0\)

=> \({{a}_{1}}=g\sin \alpha +{{a}_{0}}\cos \alpha \)

=> \({{s}_{1}}=AB=BC\cos \alpha =\left( g\sin \alpha +{{a}_{0}}\cos \alpha \right)\frac{t_{1}^{2}}{2}\)

Áp dụng định luật II Niu – tơn cho vật 2: \(\overrightarrow{{{P}_{2}}}+\overrightarrow{{{N}_{2}}}+\overrightarrow{{{F}_{qt2}}}={{m}_{2}}\overrightarrow{{{a}_{2}}}\) (4)

Chiếu (4) lên hướng chuyển động vật 2:

\({{P}_{2}}\cos \alpha -{{F}_{qt2}}\sin \alpha ={{m}_{2}}{{a}_{2}}\)=>\({{a}_{2}}=g\cos \alpha -{{a}_{0}}\sin \alpha \)=> \({{s}_{2}}=AC=BC\sin \alpha =\left( g\cos \alpha -{{a}_{0}}\sin \alpha \right)\frac{t_{2}^{2}}{2}\)

Vì t₁ = t₂ => \(\tan \alpha =\frac{g\cos \alpha -{{a}_{0}}\sin \alpha }{g\sin \alpha +{{a}_{0}}\cos \alpha }\)=> \({{a}_{0}}=\frac{1-2{{\sin }^{2}}\alpha }{\sin 2\alpha }\)

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10