Cho \(\Delta ABC\) vuông tại \(A\) có \(AB < AC\) kẻ đường cao \(AH\). Trên tia đối của tia \(HA\)
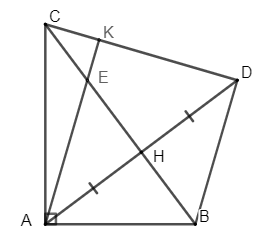
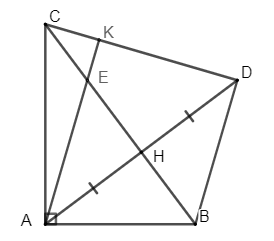
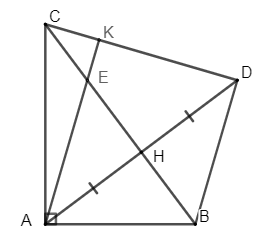
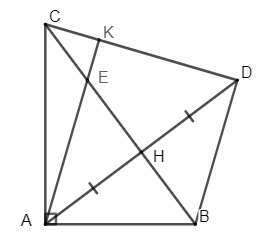
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB < AC\) kẻ đường cao \(AH\). Trên tia đối của tia \(HA\) lấy điểm \(D\) sao cho \(H{\rm{D}} = HA\).
Trả lời cho các câu 1, 2, 3, 4 dưới đây:
Áp dụng dấu hiệu nhận biết tia phân giác của một góc, dấu hiệu nhận biết hình bình hành. - Tính chất hai tam giác bằng nhau, tam giác vuông: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh ấy. -Tính chất hình bình hành.
Xét \({\Delta _v}AHB\) và \({\Delta _v}DHB\) có:
\(AH = HD\,\left( {gt} \right)\)
\(HB\) chung (gt)
\( \Rightarrow {\Delta _v}AHB = {\Delta _v}DHB\) (hai cạnh góc vuông)
Áp dụng dấu hiệu nhận biết tia phân giác của một góc, dấu hiệu nhận biết hình bình hành. - Tính chất hai tam giác bằng nhau, tam giác vuông: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh ấy. -Tính chất hình bình hành.
Vì \({\Delta _v}AHB = {\Delta _v}DHB\,\left( {cmt} \right) \Rightarrow AB = BD\) (hai cạnh tương ứng) và \(\angle ABH = \angle DBH\) (hai góc tương ứng) hay \(\angle ABC = \angle DBC\) .
Xét \(\Delta ACB\) và \(\Delta DCB\) có:
\(\begin{array}{l}AB = BD\,\left( {cmt} \right)\\\angle ABC = \angle DBC\,\left( {cmt} \right)\end{array}\)
\(BC\) chung
\( \Rightarrow \Delta ACB = \Delta DCB\,\left( {c - g - c} \right) \Rightarrow \angle ACB = \angle DCB\)(hai góc tương ứng)
\( \Rightarrow CB\) là tia phân giác của \(\angle ACD\).
Áp dụng dấu hiệu nhận biết tia phân giác của một góc, dấu hiệu nhận biết hình bình hành. - Tính chất hai tam giác bằng nhau, tam giác vuông: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh ấy. -Tính chất hình bình hành.
Vì \(AE//BD\,\left( {gt} \right) \Rightarrow \angle EAH = \angle HDB\,\left( {SLT} \right)\)
Xét \({\Delta _v}AHE\) và \({\Delta _v}DHB\) có:
\(\left\{ \begin{array}{l}AH = HD\,\left( {gt} \right)\\\angle EAH = \angle HDB\,\left( {cmt} \right)\end{array} \right. \Rightarrow {\Delta _v}AHE = {\Delta _v}DHB\) (cạnh huyền – góc nhọn)
\( \Rightarrow AE = BD\) (hai cạnh tương ứng) mà \(AE//BD\,\left( {gt} \right)\, \Rightarrow AEDB\) là hình bình hành (dấu hiệu nhận biết hình bình hành)
\( \Rightarrow DE//AB\) (tính chất hình bình hành)
Áp dụng dấu hiệu nhận biết tia phân giác của một góc, dấu hiệu nhận biết hình bình hành. - Tính chất hai tam giác bằng nhau, tam giác vuông: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh ấy. -Tính chất hình bình hành.
Vì \( \Rightarrow \Delta ACB = \Delta DCB\,\left( {cmt} \right) \Rightarrow \angle CAB = \angle CDB = {90^0}\) (hai góc tương ứng)
\( \Rightarrow \,CD \bot BD\), lại có \(AE//BD\,(gt)\, \Rightarrow \,AK \bot CD\) (do \(A,\,E,\,K\) thẳng hàng)
\( \Rightarrow \Delta AKD\) vuông tại \(K\) (dấu hiệu nhận biết tam giác vuông) (1)
Mặt khác, \(AH = HD\,\left( {gt} \right)\, \Rightarrow KH\) là đường trung tuyến của \(\Delta AKD\) (dấu hiệu nhận biết đường trung tuyến của tam giác) (2)
Từ (1) và (2) suy ra \(HK = \frac{1}{2}AD\)(trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
Quảng cáo
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 7 trên Tuyensinh247.com Học bám sát chương trình SGK mới nhất của Bộ Giáo dục. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. Phụ huynh và học sinh tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
