Một vật có khối lượng \(m=1,5kg\) trượt không vận tốc ban đầu từ đỉnh một mặt dốc dài
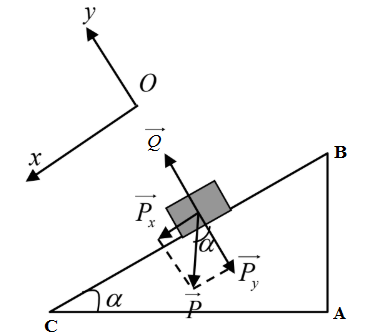
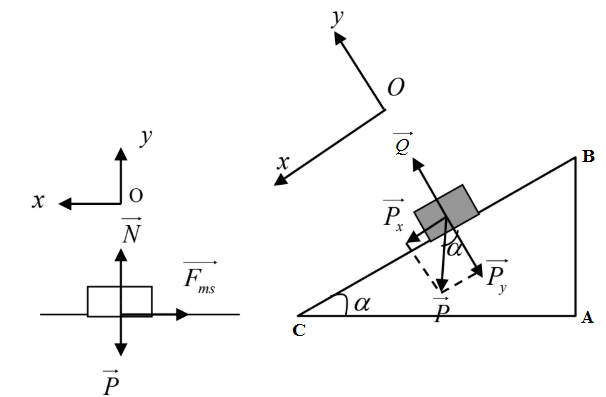
Một vật có khối lượng \(m=1,5kg\) trượt không vận tốc ban đầu từ đỉnh một mặt dốc dài \(12m\), cao \(6m\). Lấy \(g = 10m/{s^2}\).
a) Tìm động năng và vận tốc của vật khi tới chân dốc. Cho rằng lực ma sát là không đáng kể trong quá trình vật chuyển động trên mặt dốc.
b) Sau khi trượt tới chân dốc, vật tiếp tục trượt trên mặt phẳng ngang được 15m thì dừng lại. Tìm hệ số ma sát trên mặt phẳng ngang.
Đáp án đúng là: A
Quảng cáo
a) Chọn mốc tính thế năng trọng trường ở chân dốc
Áp dụng định luật bảo toàn cơ năng cho vật:
\({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}.m.{v^2} + m.g.z\)
Với z là độ cao so với mốc tính thế năng.
b) Áp dụng công thức độc lập với thời gian để xác định gia tốc của vật:
\(\;{v^2}-{v_0}^2 = 2as\)
Áp dụng phương pháp động lực học để xác định lực ma sát và tính hệ số ma sát.
Độ lớn lực ma sát: \({F_{ms}} = \mu .N\)
Tóm tắt:
\(m = {\rm{ = }}1,5kg;l = 12m;h = 6m;g = 10m/{s^2}\)
a) Tìm Wđ và v của vật khi tới chân dốc. Bỏ qua ma sát.
b) Sau khi trượt tới chân dốc, vật tiếp tục trượt trên mặt phẳng ngang được 15m thì dừng lại. Tìm hệ số ma sát trên mặt phẳng ngang.
Bài làm:
a) Chọn mốc tính thế năng ở chân dốc (tại C)
Vì vật chuyển động không ma sát nên ta có thể áp dụng định luật bảo toàn cơ năng cho vật. Ta có:
\(\begin{array}{l}
{{\rm{W}}_B} = {{\rm{W}}_C} \Rightarrow m.g.h = \frac{1}{2}.m.v_C^2\\
\Rightarrow {v_C} = \sqrt {2g.h} = \sqrt {2.10.6} = 2\sqrt {30} \left( {m/s} \right)
\end{array}\)
Động năng của vật tại C là:
\({{\rm{W}}_C} = \frac{1}{2}.m.v_C^2 = \frac{1}{2}.1,5.{\left( {2\sqrt {30} } \right)^2} = 90\left( J \right)\)
b) Ta có hình vẽ
Khi vật chuyển động trên mặt sàn nằm ngang, ta biểu diễn các lực tác dụng vào vật như hình vẽ.
Chọn hệ tọa độ Oxy như trên hình vẽ.
Áp dụng công thức độc lập với thời gian, ta có:
\({v^2} - v_C^2 = 2.a.s \Rightarrow 0 - {(2\sqrt {30} )^2} = 2.a.15 \Rightarrow a = - 4\left( {m/{s^2}} \right)\)
Áp dụng định luật II Niu – tơn cho vật ta có:
\(\overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = m.\overrightarrow a \) (*)
Chiếu phương trình (*) lên Oxy ta có:
\(\left\{ \begin{array}{l}
N - P = 0\\
{F_{ms}} = m.a
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
N = P = mg = 1,5.10 = 15N\\
{F_{ms}} = 1,5.4 = 6 = \mu .N
\end{array} \right. \Rightarrow \mu = \frac{{{F_{ms}}}}{N} = \frac{6}{{15}} = 0,4\)
Vậy hệ số ma sát bằng 0,4.
Đáp án cần chọn là: A
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
