Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Cho hình tam giác ABC có chiều cao hạ từ đỉnh A là 12 cm, chiều cao đó bằng \(\frac{3}{4}\) độ
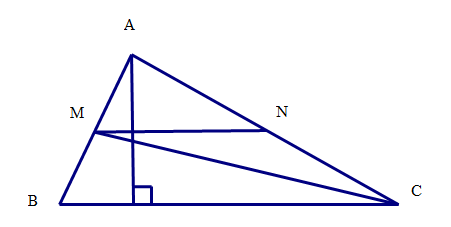
Cho hình tam giác ABC có chiều cao hạ từ đỉnh A là 12 cm, chiều cao đó bằng \(\frac{3}{4}\) độ dài đáy tương ứng . Gọi M, N lần lượt là trung điểm của cạnh AB và AC. Nối M với C, nối M với N.
a) Tính diện tích tam giác ABC
b) Tính diện tích hình tứ giác MNCB
Đáp án đúng là: A
Quảng cáo
a) Áp dụng công thức tính diện tích hình tam giác : \(\)\(S{\rm{ }} = {\rm{ }}a \times \;h\)
Trong đó:
S: diện tích
h: Chiều cao
a: cạnh đáy tương ứng
b) Chia hình MNCN thành hai tam giác nhỏ. Lần lượt tính diện tích của hai tam giác ấy rồi cộng lại với nhau.
a) Độ dài cạnh đáy BC là:
\(12\,\,:\,\,\frac{3}{4}\,\, = \,\,16\,\,\left( {cm} \right)\)
Diện tích tam giác ABC là:
\(S\,\, = \,\,\frac{1}{2}\,\, \times \,\,12\,\, \times \,\,16\,\, = \,\,96\,\,\left( {c{m^2}} \right)\)
Đáp số: \(96c{m^2}.\)
b) Vì M là trung điểm của AB nên \(AM{\rm{ }} = {\rm{ }}MB\)
Suy ra \({S_{MAC}} = {S_{MBC}}\) (chung đường cao hạ từ C)
Mà \({S_{MAC}} + {S_{MBC}} = {S_{ABC}}\)
Nên
\(\begin{array}{l}{S_{BMC}} = {S_{MAC}} = \frac{1}{2}\,\, \times {S_{ABC}}\\\,\,\,\,\,\,\,\,\,\,\, = \,\,\frac{1}{2}\,\,\, \times \,\,96\,\, = \,\,48\,\,\left( {c{m^2}} \right)\end{array}\)
Vì N là trung điểm của AC nên \(AN{\rm{ }} = {\rm{ }}NC\)
Suy ra \({S_{MAN}} = {S_{MCN}}\) (chung đường cao hạ từ M)
Mà \({S_{MAN}} + {S_{MCN}} = {S_{AMC}}\)
Suy ra:
\({S_{MAN}} = {S_{MNC}} = \frac{1}{2}\,\, \times {S_{AMC}}\)
\( = \frac{1}{2} \times 48 = 24(c{m^2})\)
Ta có:
\({S_{MNBC}} = {S_{BMC}} + {S_{MNC}} = 48{\rm{ }} + {\rm{ }}24 = 72(c{m^2})\)
Đáp số: \(72c{m^2}.\)
Tham Gia Group Dành Cho 2K14 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến các môn Toán, Tiếng Việt, Tiếng Anh lớp 5 trên Tuyensinh247.com cam kết giúp con lớp 5 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
