Một vật trượt không vận tốc đầu từ đỉnh của một mặt phẳng nghiêng dài L = 10m, góc
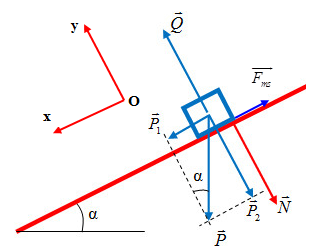
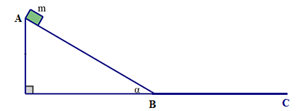
Một vật trượt không vận tốc đầu từ đỉnh của một mặt phẳng nghiêng dài L = 10m, góc nghiêng \(\alpha = {30^0}\). Lấy \(g = 10m/{s^2}\), hệ số ma sát giữa vật và mặt phẳng nghiêng là 0,2. Tính gia tốc và vận tốc của vật tại chân mặt phẳng nghiêng.
Đáp án đúng là: B
Quảng cáo
Phương pháp: động lực học:
Bước 1: Chọn vật (hệ vật) khảo sát.
Bước 2: Chọn hệ quy chiếu (Cụ thể hoá bằng hệ trục toạ độ vuông góc; Trục toạ độ Ox luôn trùng với phương chiều chuyển động; Trục toạ độ Oy vuông góc với phương chuyển động)
Bước 3: Xác định các lực và biểu diễn các lực tác dụng lên vật trên hình vẽ.
Bước 4: Viết phương trình hợp lực tác dụng lên vật theo định luật II Niu Tơn.
\(\overrightarrow {{F_{hl}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... + \overrightarrow {{F_n}} = m.\vec a\) (*) (Tổng tất cả các lực tác dụng lên vật)
Bước 5: Chiếu phương trình lực (*) lên các trục toạ độ Ox, Oy:
\(\left\{ {\begin{array}{*{20}{l}}
{Ox:{F_{1x}} + {F_{2x}} + \ldots + {F_{nx}} = ma\,\,\,\,\left( 1 \right)}\\
{Oy:{F_{1y}} + {F_{2y}} + \ldots + {F_{ny}} = 0\,\,\,\,\,\,\,\left( 2 \right)}
\end{array}} \right.\)
Giải phương trình (1) và (2) ta thu được đại lượng cần tìm
Vật chịu tác dụng của 3 lực trên mặt phẳng nghiêng: Trọng lực \(\vec P\); Phản lực \(\vec Q\); Lực ma sát: \(\overrightarrow {{F_{ms}}} \)
Biểu diễn các lực tác dụng vào vật và chọn hệ trục toạ độ như hình vẽ:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\vec P = \overrightarrow {{P_1}} + \overrightarrow {{P_2}} }\\{\left( {\overrightarrow {{P_2}} ;\vec P} \right) = \alpha }\end{array}} \right.\)
Từ hình vẽ ta có:
\(\left\{ {\begin{array}{*{20}{l}}{\sin \alpha = \dfrac{{{P_1}}}{P} \Rightarrow {P_1} = P.\sin \alpha = mg.\sin \alpha }\\{\cos \alpha = \dfrac{{{P_2}}}{P} \Rightarrow {P_2} = P.\cos \alpha = mg.\cos \alpha }\end{array}} \right.\)
Áp dụng định luật II Niuton ta có :
\(\overrightarrow {{F_{ms}}} + \vec Q + \overrightarrow {{P_1}} + \overrightarrow {{P_2}} = m.\vec a{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( * \right)\)
Chiếu (*) lên Ox, Oy ta được :
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{ - {F_{ms}} + {P_1} = ma}\\{Q - {P_2} = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \dfrac{{{P_1} - {F_{ms}}}}{m}}\\{Q = {P_2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \dfrac{{mg.\sin \alpha - \mu N}}{m}}\\{N = Q = {P_2} = mg.\cos \alpha }\end{array}} \right.}\\{ \Rightarrow a = \dfrac{{mg.\sin \alpha - \mu .mg.\cos \alpha }}{m} = g\left( {\sin \alpha - \mu .\cos \alpha } \right)}\end{array}\)
Thay số ta được : \(a = 10.\left( {\sin 30 - 0,2.\cos 30} \right) = 3,27m/{s^2}\)
Ta có : \(v_B^2 - v_A^2 = 2a.AB\)
\( \Rightarrow {v_B} = \sqrt {v_A^2 + 2a.AB} = \sqrt {0 + 2.4,13.10} \approx 8,1m/s\)
Đáp án cần chọn là: B
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
