Con lắc lò xo được đặt trên mặt bàn nằm ngang có hệ số ma sát là \(\mu = \dfrac{1}{{\sqrt

Câu hỏi số 558865:

Vận dụng cao

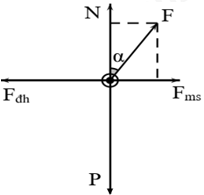
Con lắc lò xo được đặt trên mặt bàn nằm ngang có hệ số ma sát là \(\mu = \dfrac{1}{{\sqrt 3 }}\). Vật được tích điện q và đặt toàn bộ hệ dao động trong một điện trường đều có cường độ điện trường E. Kéo vật đến vị trí lò xo giãn một đoạn b rồi buông nhẹ. Nếu điện trường có phương thẳng đứng và hướng lên trên thì tốc độ cực đại của vật sau khi thả là 60cm/s. Nếu điện trường có phương thẳng đứng và hướng xuống thì tốc độ cực đại của vật sau khi thả là 40cm/s. Nếu điện trường có hướng như hình vẽ thì tốc độ cực đại của vật sau khi thả là 50cm/s. Tính góc lệch của điện trường so với phương thẳng đứng trong trường hợp này.

A. \({60^0}\)

B. \({15^0}\)

C. \({30^0}\)

D. \({45^0}\)

Đáp án đúng là: C

Quảng cáo

Xem lời giải

Câu hỏi:558865

Phương pháp giải

Định luật II Niuton: \(\overrightarrow F = m\overrightarrow a \)

Tốc độ dao động cực đại: \({v_{\max }} = A\omega \)

Giải chi tiết

Các lực tác dụng lên vật:

Áp dụng định luật II Niutơn tại VTCB mới ta có:

\(\left\{ \begin{array}{l}{F_{ms}} + F\sin \alpha - k\Delta {l_0} = 0\\N + F.\cos \alpha - mg = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\Delta {l_0} = \dfrac{{\mu N + F\sin \alpha }}{k}\\N = mg - F.\cos \alpha \end{array} \right.\)

\( \Rightarrow \Delta {l_0} = \dfrac{{\mu \left( {mg - F\cos \alpha } \right) + F\sin \alpha }}{k}\)

\( \Rightarrow \Delta {l_0} = \dfrac{{\mu mg}}{k} + \dfrac{F}{k}\left( {\sin \alpha - \mu \cos \alpha } \right)\)

Tốc độ cực đại: \({v_{\max }} = \omega A' = \omega \left( {b - \Delta {l_0}} \right)\)

\( \Rightarrow {v_{\max }} = \omega \left[ {b - \dfrac{{\mu mg}}{k} - \dfrac{F}{k}\left( {\sin \alpha - \mu \cos \alpha } \right)} \right] = 50\,\,\left( 1 \right)\)

Khi: \(\alpha = 0 \Rightarrow {v_{ma{\rm{x}}}} = \omega \left( {b - \dfrac{{\mu mg}}{k} + \dfrac{F}{k}\mu } \right) = 60\,\,\left( 2 \right)\)

Khi \(\alpha = {180^0} \Rightarrow {v_{\max }} = \omega \left( {b - \dfrac{{\mu mg}}{k} - \dfrac{F}{k}\mu } \right) = 40\,\,\left( 3 \right)\)

Từ (2) và (3) \( \Rightarrow \left\{ \begin{array}{l}\omega \left( {b - \dfrac{{\mu mg}}{k}} \right) = 50\\\omega \dfrac{F}{k}\mu = 10\end{array} \right.\)

Thay vào (1) ta được: \(50 - \dfrac{{10}}{\mu }\left( {\sin \alpha - \mu \cos \alpha } \right) = 50\)

\( \Rightarrow \sin \alpha - \mu \cos \alpha = {\rm{0}}\)

\( \Rightarrow {\rm{tan}}\alpha = \mu = \dfrac{1}{{\sqrt 3 }} \Rightarrow \alpha = {30^0}\)

Đáp án cần chọn là: C

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.