Cho mạch điện như hình vẽ. Điện áp giữa hai đầu AB ổn định có biểu thức \(u = {U_0}\cos

Câu hỏi số 570439:

Vận dụng cao

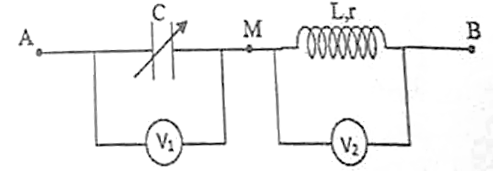
Cho mạch điện như hình vẽ. Điện áp giữa hai đầu AB ổn định có biểu thức \(u = {U_0}\cos \omega t\,\,\left( V \right)\). Cuộn dây không thuần cảm, tỷ số \(\dfrac{r}{L} = \sqrt 3 \omega \), tụ điện có điện dung C thay đổi được. Các vôn kế nhiệt có điện trở rất lớn. Điều chỉnh \(C = {C_1}\) thì tổng số chỉ của hai vôn kế lớn nhất bằng 200 V. Điều chỉnh \(C = {C_2}\) để số chỉ vôn kế \({V_1}\) đạt cực đại thì công suất tiêu thụ là 100W. Điều chỉnh \(C = {C_3}\) thì cường độ dòng điện hiệu dụng đạt giá trị cực đại là

A. 4A.

B. 2A.

C. \(2\sqrt 3 A\).

D. \(2\sqrt 2 A\).

Đáp án đúng là: C

Quảng cáo

Xem lời giải

Câu hỏi:570439

Phương pháp giải

Tổng trở: \(Z = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)

Sử dụng phương pháp chuẩn hóa số liệu

Điện áp giữa hai đầu đoạn mạch: \(U = IZ\)

Bất đẳng thức Cauchy: \(a + b \ge 2\sqrt {ab} \) (dấu “=” xảy ra \( \Leftrightarrow a = b\))

Công suất tiêu thụ: \(P = {I^2}r\)

Giải chi tiết

Theo đề bài ta có tỉ số:

\(\dfrac{r}{L} = \sqrt 3 \omega \Rightarrow r = \sqrt 3 \omega L = \sqrt 3 {Z_L}\)

Chuẩn hóa \({Z_L} = 1 \Rightarrow r = \sqrt 3 \)

Khi \(C = {C_1}\), tổng số chỉ hai vôn kế là:

\(\begin{array}{l}{U_t} = {U_{{V_1}}} + {U_{{V_2}}} = {U_{{C_1}}} + {U_{Lr}}\\ \Rightarrow {U_t} = \dfrac{{U\left( {{Z_{{C_1}}} + \sqrt {{r^2} + {Z_L}^2} } \right)}}{{\sqrt {{r^2} + {{\left( {{Z_L} - {Z_{{C_1}}}} \right)}^2}} }} = \dfrac{{U\left( {{Z_{{C_1}}} + 2} \right)}}{{\sqrt {3 + {{\left( {{Z_{{C_1}}} - 1} \right)}^2}} }}\\ \Rightarrow {U_t}^2 = \dfrac{{{U^2}\left( {{Z_{{C_1}}}^2 + 2{Z_{{C_1}}} + 4} \right)}}{{{Z_{{C_1}}}^2 - 2{Z_{{C_1}}} + 4}} = {U^2}\left( {1 + \dfrac{{4{Z_{{C_1}}}}}{{{Z_{{C_1}}}^2 - 2{Z_{{C_1}}} + 4}}} \right)\\ \Rightarrow {U_t}^2 = {U^2}\left( {1 + \dfrac{4}{{{Z_{{C_1}}} + \dfrac{4}{{{Z_{{C_1}}}}} - 2}}} \right)\end{array}\)

Để \({U_{t\max }} \Rightarrow {\left( {{Z_{{C_1}}} + \dfrac{4}{{{Z_{{C_1}}}}} - 2} \right)_{\min }} \Rightarrow {\left( {{Z_{{C_1}}} + \dfrac{4}{{{Z_{{C_1}}}}}} \right)_{\min }}\)

Áp dụng bất đẳng thức Cauchy, ta có:

\(\begin{array}{l}{Z_{{C_1}}} + \dfrac{4}{{{Z_{{C_1}}}}} \ge 2\sqrt {{Z_{{C_1}}}.\dfrac{4}{{{Z_{{C_1}}}}}} \\ \Rightarrow {\left( {{Z_{{C_1}}} + \dfrac{4}{{{Z_{{C_1}}}}}} \right)_{\min }} \Leftrightarrow {Z_{{C_1}}} = \dfrac{4}{{{Z_{{C_1}}}}} \Rightarrow {Z_{{C_1}}} = 2\end{array}\)

Khi đó ta có:

\({U_t}^2 = {U^2}\left( {1 + \dfrac{4}{{4 - 2}}} \right) = 3{U^2} \Rightarrow {200^2} = 3{U^2} \Rightarrow U = \dfrac{{200}}{{\sqrt 3 }}\,\,\left( V \right)\)

Số chỉ vôn kế \({V_1}\) đạt cực đại khi:

\({Z_{{C_2}}} = \dfrac{{{r^2} + {Z_L}^2}}{{{Z_L}}} = \dfrac{{3 + 1}}{1} = 4\)

Công suất tiêu thụ trong mạch khi đó là:

\(\begin{array}{l}{P_2} = \dfrac{{{U^2}r}}{{{r^2} + {{\left( {{Z_L} - {Z_{{C_2}}}} \right)}^2}}} \Rightarrow 100 = {\left( {\dfrac{{200}}{{\sqrt 3 }}} \right)^2}.\dfrac{{\sqrt 3 {Z_L}}}{{3{Z_L}^2 + {{\left( {1 - 4} \right)}^2}{Z_L}^2}}\\ \Rightarrow 100 = \dfrac{{10000}}{{3\sqrt 3 {Z_L}}} \Rightarrow {Z_L} = \dfrac{{100}}{{3\sqrt 3 }}\,\,\left( \Omega \right)\\ \Rightarrow r = \sqrt 3 {Z_L} = \dfrac{{100}}{3}\,\,\left( \Omega \right)\end{array}\)

Khi \(C = {C_3}\), cường độ hiệu dụng trong mạch đạt giá trị cực đại là:

\({I_{\max }} = \dfrac{U}{r} = \dfrac{{200}}{{\sqrt 3 }}.\dfrac{3}{{100}} = 2\sqrt 3 \,\,\left( A \right)\)

Đáp án cần chọn là: C

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.