Bác Thu và bác Tuệ ghi lại số cuộc điện thoại mà mỗi người gọi mỗi ngày trong 10 ngày

Câu hỏi số 591994:

Vận dụng

Bác Thu và bác Tuệ ghi lại số cuộc điện thoại mà mỗi người gọi mỗi ngày trong 10 ngày được lữa chọn ngẫu nhiên từ tháng 1/2022 ở bảng sau:

a) Hãy tìm số trung vị, tứ phân vị và mốt của số cuộc điện thoại và mỗi bác gọi theo số liệu trên.

b) Nếu so sánh theo số trung bình thì ai có nhiều cuộc điện thoại hơn.

c) Nếu so sánh theo số trung vị thì ai có nhiều cuộc điện thoại hơn.

Quảng cáo

Xem lời giải

Câu hỏi:591994

Phương pháp giải

* Số trung bình của mẫu số liệu \({x_1},\,\,{x_2},\,\,....,\,\,{x_n}\) kí hiệu là \(\bar x\), được tính bằng công thức:

\(\bar x = \dfrac{{{m_1}{x_2} + {m_2}{x_2} + ... + {m_k}{x_k}}}{n}\)

Trong đó m_k là tần số của giá trị x_k và \(n = {m_1} + {m_2} + ... + {m_k}\).

* Tứ phân vị của mẫu số liệu:

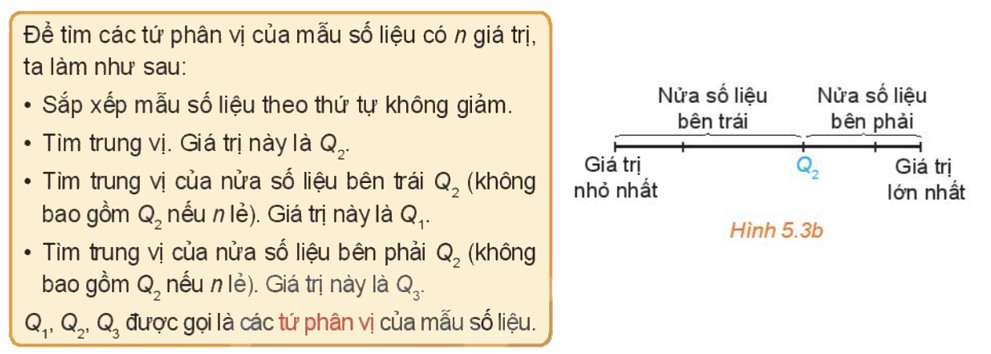
* Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất.

b) So sánh số trung bình và kết luận ai có số trung bình lớn hơn thì gọi được nhiều cuộc điện thoại mỗi ngày hơn.

c) Tính số trung vị \({M_e} = {Q_2}\). So sánh và kết luận ai có số trung vị lớn hơn thì gọi được nhiều cuộc điện thoại mỗi ngày hơn.

Giải chi tiết

* Số trung bình của số cuộc đinệ thoại mà mỗi bác gọi là:

Bác Thu: \(\overline {{x_1}} = \dfrac{{2 + 7 + 3 + 6 + 1 + 4 + 1 + 4 + 5 + 1}}{{10}} = 3,4\).

Bác Tuệ: \(\overline {{x_2}} = \dfrac{{1 + 3 + 1 + 2 + 3 + 4 + 1 + 2 + 20 + 2}}{{10}} = 3,9\)

* Tìm tứ phân vị:

Bác Thu:

Sắp xếp mẫu theo thứ tự không giảm ta được: 1 1 1 2 3 4 4 5 6 7.

Cỡ mẫu là n = 10 chẵn nên giá trị tứ phân vị thứ hai là \({Q_{{2_1}}} = \dfrac{1}{2}\left( {3 + 4} \right) = 3,5\).

Tứ phân vị thứ nhất là trung vị của mẫu 1 1 1 2 3. Do đó \({Q_{{1_1}}} = 1\).

Tứ phân vị thứ ba là trung vị của mẫu 4 4 5 6 7. Do đó \({Q_{{3_1}}} = 5\).

Bác Tuệ:

Sắp xếp mẫu theo thứ tự không giảm ta được: 1 1 1 2 2 2 3 3 4 20.

Cỡ mẫu là n = 10 chẵn nên giá trị tứ phân vị thứ hai là \({Q_{{2_2}}} = \dfrac{1}{2}\left( {2 + 2} \right) = 2\).

Tứ phân vị thứ nhất là trung vị của mẫu 1 1 1 2 2 . Do đó \({Q_{{1_2}}} = 1\).

Tứ phân vị thứ ba là trung vị của mẫu 2 3 3 4 20. Do đó \({Q_{{3_2}}} = 3\).

b) Ta có: \(\overline {{x_1}} < \overline {{x_2}} \) nên nếu so sánh theo số trung bình thì bác Tuệ có nhiều cuộc điện thoại hơn.

c) Số trung vị của số cuộc điện thoại mà bác Thu gọi là: \({M_{{e_1}}} = {Q_{{2_1}}} = 3,5\).

Số trung vị của số cuộc điện thoại mà bác Tuệ gọi là: \({M_{{e_2}}} = {Q_{{2_2}}} = 2\).

Do đó nếu so sánh theo số trung bình thì bác Thu có nhiều cuộc điện thoại hơn.

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.