Cho tam giác ABC có M thuộc cạnh AC sao cho \({\rm{AM}} = {\rm{CM}}\), N thuộc cạnh BC sao cho \({\rm{BN}} =

Câu hỏi số 610477:

Vận dụng cao

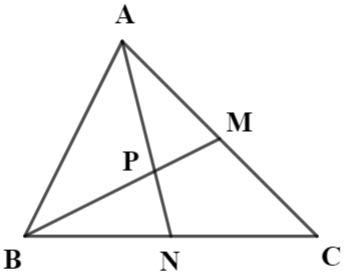
Cho tam giác ABC có M thuộc cạnh AC sao cho \({\rm{AM}} = {\rm{CM}}\), N thuộc cạnh BC sao cho \({\rm{BN}} = {\rm{CN}}\), P là giao điểm của hai đoạn thẳng AN và BM. Tính tỉ số diện tích tam giác BPN và tam giác APM.

A. \(\dfrac{1}{4}\)

B. \(\dfrac{1}{3}\)

C. \(\dfrac{1}{2}\)

D. \(1\)

Đáp án đúng là: D

Quảng cáo

Xem lời giải

Câu hỏi:610477

Phương pháp giải

\({{\rm{S}}_{{\rm{ABM}}}} = {{\rm{S}}_{{\rm{ABN}}}} = \dfrac{1}{2}{{\rm{S}}_{{\rm{ABC}}}}\) nên \({{\rm{S}}_{{\rm{APM}}}} = {{\rm{S}}_{{\rm{BPN}}}}\). Vậy \(\dfrac{{{{\rm{S}}_{{\rm{APM}}}}}}{{{{\rm{S}}_{{\rm{BPN}}}}}} = 1\)

Giải chi tiết

\({{\rm{S}}_{{\rm{ABM}}}} = \dfrac{1}{2}{{\rm{S}}_{{\rm{ABC}}}}\) (vì có chung đường cao kẻ từ B và đáy \({\rm{AM}} = \dfrac{1}{2}{\rm{AC}}\))

\({{\rm{S}}_{{\rm{ABN}}}} = \dfrac{1}{2}{{\rm{S}}_{{\rm{ABC}}}}\) (vì có chung đường cao kẻ từ A và đáy \({\rm{BN}} = \dfrac{1}{2}{\rm{BC}}\))

Suy ra: \({{\rm{S}}_{{\rm{ABM}}}} = {{\rm{S}}_{{\rm{ABN}}}}\) hay \({{\rm{S}}_{{\rm{ABP}}}} + {{\rm{S}}_{{\rm{APM}}}} = {{\rm{S}}_{{\rm{ABP}}}} + {{\rm{S}}_{{\rm{BPN}}}}\)

Suy ra: \({{\rm{S}}_{{\rm{APM}}}} = {{\rm{S}}_{{\rm{BPN}}}}\)

Vậy: \(\dfrac{{{{\rm{S}}_{{\rm{APM}}}}}}{{{{\rm{S}}_{{\rm{BPN}}}}}} = 1\).

Đáp án cần chọn là: D

Tham Gia Group Dành Cho 2K14 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến các môn Toán, Tiếng Việt, Tiếng Anh lớp 5 trên Tuyensinh247.com. Cam kết giúp con lớp 5 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link