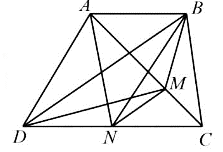
Cho hình thang ABCD, lấy điểm M trên đường chéo AC sao cho AM = 2 × MC.Lấy điểm N trên cạnh CD sao
Cho hình thang ABCD, lấy điểm M trên đường chéo AC sao cho AM = 2 × MC.
Lấy điểm N trên cạnh CD sao cho BDNM là hình thang.
a) So sánh diện tích hai tam giác BDN và BDM.
b) Tính tỉ số \(\dfrac{{{S_{ABND}}}}{{{S_{BNC}}}}\)
Quảng cáo
a) So sánh chiều cao của hai tam giác có chung đáy BD.
b) Dựa vào chiều cao và đáy của các tam giác để tìm tỉ số.
a) Vì BDNM là hình thang nên SBDN = SBMD (hai tam giác có chung đáy BD, chiều cao hạ từ N xuống BD bằng chiều cao hạ từ M xuống BD cùng bằng chiều cao hình thang BDNM ).
b) Vì AM = 2 × MC nên SABM = 2 x SBMC (hai tam giác có chung chiều cao hạ từ B xuống AC).
Vì AM = 2 × MC nên SANM = 2 x SMNC (hai tam giác có chung chiều cao hạ từ N xuống AC).
Suy ra SABMN = SABM + SANM = 2 x SBMC + 2 x SMNC = 2 x (SBMC + SMNC)
Mà SABMN = SNAB + SNMB và SNAB = SDAB nên SDAB + SNMB = 2 x (SBMC + SMBC)
\( \Rightarrow \)SDAB = 3 x SNMB = 2 x (SBMC +SMNC + SNMB) = 2 x SBNC (1)
Lại có SADC = 3 x SMDC (hai tam giác có chung chiều cao hạ từ D xuống AC và AM = 2 x MC)
Mà hai tam giác này có chung đáy CD nên chiều cao hạ từ A xuống CD gấp 3 lần chiều cao hạ từ M xuống CD.
Mặt khác, chiều cao hạ từ A xuống CD bằng chiều cao hạ từ B xuống CD
\( \Rightarrow \) Chiều cao hạ từ B xuống CD gấp 3 lần chiều cao hạ từ M xuống CD.
Do đó SBDN = 3 x SMDN
Vì BDNM là hình thang nên SMDN = SNMB \( \Rightarrow \)SBDN = 3 x SNMB
Thay vào (1) ta được SDAB + SBDN = 2 x SBNC
\( \Rightarrow \) SABND = 2 x SBNC \( \Rightarrow \) \(\dfrac{{{S_{ABND}}}}{{{S_{BNC}}}} = 2\)
Tham Gia Group Dành Cho 2K14 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến các môn Toán, Tiếng Việt, Tiếng Anh lớp 5 trên Tuyensinh247.com. Cam kết giúp con lớp 5 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
