Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

Các thiên thạch có đường kính \(140m\)và có thể lại gần

Câu hỏi số 730741:
Vận dụng

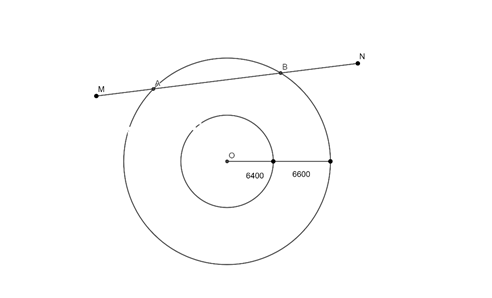
Các thiên thạch có đường kính \(140m\)và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn \(7500000km\)được coi lf những vật thể có khả năng va chạm và gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, người ta đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất. Giả sử có một hệ thống quan sát có khả năng theo dõi các vật thể ở độ cao không vượt quá \(6600km\) so với mực nước biển. Coi Trái Đất là khối cầu có bán kính \(6400km\). Chọn hệ trục tọa độ \(Oxyz\) trong không gian có gốc \(O\) tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là \(1000km\). Một thiên thạch chuyển động ( coi như một hạt) với tốc độ không đổi theo một đường thẳng tử điểm \(M(6;20;0)\) đến điểm \(N( - 6; - 12;16)\).

Đúng Sai
a)

Đường thẳng \(MN\) có phương trình tham số là \(\left\{ \begin{array}{l}x = 6 + 3t\\y = 20 + 8t\\z =  - 4t\end{array} \right.,(t \in \mathbb{R})\)
b)

Vị trí đầu tiên thiên thạch di chuyển vào phạm vi theo dõi của hệ thống quan sát là điểm \(A( - 3; - 4;12)\).
c)

Khoảng cách giữa vị trí đàu tiên và ví trí cuối cùng mà thiên thạch di chuyển  trong phạm vi theo dõi của hệ thống quan sát là \(18900km\)( kết quả làm tròn đến hàng trăm theo đơn vị ki-lô-mét).
d)

Nếu thời gian di chuyển của thiên thạch trong phạm vi theo dõi của hệ thống quan sát là 3 phút thì giời gian nó di chuyển từ \(M\)đến \(N\)là 6 phút.

Đáp án đúng là: Đ; S; Đ; Đ

Quảng cáo

Xem lời giải
Câu hỏi:730741
Giải chi tiết

a) Đúng: Ta có \(\overrightarrow {MN}  = (3;8; - 4)\).

Có phương trình đường thẳng đi qua \(M(6;20;0)\)và có vecto chỉ phương mà \(\overrightarrow {MN} \).

Vậy đường thẳng \(MN\) có phương trình tham số là:

\(d: \left\{ \begin{array}{l}x = 6 + 3t\\y = 20 + 8t\\z =  - 4t\end{array} \right.,(t \in \mathbb{R})\)

b) Sai: Ta có phương trình mặt cầu mà hệ thống quan sát theo dõi được các vật thể:

Có tâm \(O(0;0;0)\) và bán kính là \(R = 6,4 + 6,6 = 13.\)

Suy ra ta có phương trình :  \((C)\): \({x^2} + {y^2} + {z^2} = {13^2} = 169\)

Khi đó điểm đầu và điểm cuối mà thiên thạch di chuyển trong phạm vi theo dõi của hệ thống quan sát là nghiệm của phương trình giao điểm của đường thẳng \(MN\) và mặt cầu \((C)\)

Suy ra : \({\left( {6 + 3t} \right)^2} + {(20 + 8)^2} + {( - 4t)^2} = 169\)

Giải phương trình trên ta có: \(89t + 256t + 267 = 0 \Leftrightarrow \left[ \begin{array}{l}t =  - 1\\t =  - 3\end{array} \right.\)

Ta được hai điểm \(A( - 3; - 4;12)\) và \(B\left( {3;12;4} \right)\).

Tuy nhiên, ta có khoảng cách \(MA = 3\sqrt {89}  \approx 28.3\) và \(MB = \sqrt {89}  \approx 9.4\).

Vậy vị trí đầu tiên thiên thạch di chuyển vào phạm vi theo dõi là \(B\left( {3;12;4} \right)\).

Vậy vị trí cuối cùng thiên thạch di chuyển vào phạm vi theo dõi là \(A( - 3; - 4;12)\)

c) Đúng: Khoảng cách \(AB = MB - MA = 2\sqrt {89}  \approx 18,9\)

Vậy khoảng cách thực tế giữa \(AB\)là \( \approx 18900km\).

d) Đúng: Ta có khoảng cách \(MN = \sqrt {{{12}^2} + {{32}^2} + {{16}^2}}  = 4\sqrt {89} \)

Ta thấy \(MN = 2AB \Rightarrow \dfrac{{MN}}{{AB}} = 2\) mà vận tốc của thiên thạch không đổi ta có thời gian cũng tỷ lệ với khoảng cách.

Khi đó: \(\dfrac{{MN}}{{AB}} = \dfrac{6}{3} = 2\).

Đáp án cần chọn là: Đ; S; Đ; Đ

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn