Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 1 - Ngày 20-21/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

Đồng hồ mặt trời là một công cụ đo thời gian cổ xưa, hoạt động dựa trên

Câu hỏi số 744403:
Vận dụng

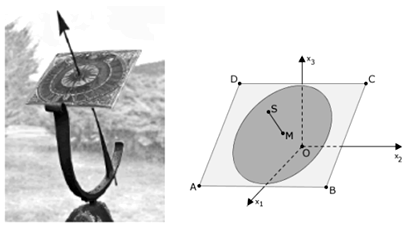
Đồng hồ mặt trời là một công cụ đo thời gian cổ xưa, hoạt động dựa trên bóng đổ của ánh sáng mặt trời. Cấu tạo cơ bản của một đồng hồ mặt trời bao gồm: Một kim đồng hồ (Gnomon) được đặt nghiêng sao cho nó chỉ về phía cực Bắc; một mặt số (Dial) là mặt phẳng nơi bóng của kim đồng hồ rơi xuống và hiển thị thời gian. Một đồng hồ mặt trời được mô hình hóa trong không gian Oxyz. Hình chữ nhật ABCD với \(A(5; - 4;0)\) và \(B(5;4;0)\) biểu diễn mặt số của đồng hồ. Kim đồng hồ được biểu diễn với đoạn thẳng MS với \(S\left( {\dfrac{9}{2};0;\dfrac{9}{2}} \right)\) và \(M\left( {\dfrac{5}{2};0;2} \right)\) là trung điểm đường chéo của hình chữ nhật ABCD. Mỗi đơn vị độ dài trong hệ tọa độ ứng với 10cm trong thực tế. (Nguồn: Abitur 2015 Mathematik Geometrie VI)

Đúng Sai
a)

a) Tọa độ điểm C là \(C\left( {0; - 4; - 4} \right)\).
b) Mặt số của đồng hồ có phương trình: \(4x + 5y - 20 = 0\).
c) Kim đồng hồ có chiều dài 32cm và vuông góc với mặt số của đồng hồ.
d) Mặt đồng hồ được đặt nghiêng so với mặt đất (mặt phẳng \(Oxy\)) một góc \(\alpha \). Để đồng hồ mặt trời hiển thị thời gian chính xác thì điều kiện \(\alpha  + \beta  = {90^o}\) cần được thỏa mãn, trong đó \(\beta \) là vĩ độ của nơi đặt đồng hồ. Khi đó ta có \(\beta  \approx {40^o}.\)  

Đáp án đúng là: S; S; Đ; S

Quảng cáo

Xem lời giải
Câu hỏi:744403
Phương pháp giải

a) Có \(M\) là trung điểm \(AC\), từ đó suy ra toạ độ điểm \(C\).

b) Viết phương trình mặt phẳng \(ABCD\) khi biết cặp vectơ chỉ phương \(\overrightarrow {AB}\), \(\overrightarrow {AM} \).

c) Tính độ dài \(MS\), kiểm tra \(\overrightarrow {MS}\) và \(\overrightarrow {{n_1}} \) có cùng phương hay không.

d) Tính góc giữa hai mặt phẳng: \(\cos \alpha  = \dfrac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\) với \(\overrightarrow {{n_1}}\) và \(\overrightarrow {{n_2}}\) là các vectơ pháp tuyến của hai mặt phẳng.

Giải chi tiết

a) Sai: Ta có \(A(5; - 4;0)\), \(M\left( {\dfrac{5}{2};0;2} \right)\)\( \Rightarrow \overrightarrow {AM} \left( {\dfrac{{ - 5}}{2};4;2} \right)\).

Có \(M\) là trung điểm của \(AC\), suy ra:

\(\overrightarrow {AC}  = 2\overrightarrow {AM}  \Rightarrow \left\{ \begin{array}{l}{x_C} = {x_A} + 2.\dfrac{{ - 5}}{2}\\{y_C} = {y_A} + 2.4\\{z_C} = {z_A} + 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 5 - 5\\{y_C} =  - 4 + 8\\{z_C} = 0 + 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 0\\{y_C} = 4\\{z_C} = 4\end{array} \right.\)

Vậy \(C\left( {0;4;4} \right)\).

b) Sai: Có \(A(5; - 4;0)\), \(B(5;4;0)\)\( \Rightarrow \overrightarrow {AB} \left( {0;8;0} \right)\)

Mặt số của đồng hồ là mặt phẳng \(\left( {ABCD} \right)\), \(\left( {ABCD} \right)\) nhận \(\overrightarrow {AB} ,\overrightarrow {AM} \) làm cặp vectơ chỉ phương.

Ta có \(\left[ {\overrightarrow {AB} ,\overrightarrow {AM} } \right] = \left( {16;0;20} \right)\), suy ra vectơ pháp tuyến của mặt phẳng \(\left( {ABCD} \right)\) đi qua \(A(5; - 4;0)\) và nhận  \(\overrightarrow {{n_1}}  = \dfrac{1}{4}\left[ {\overrightarrow {AB} ,\overrightarrow {AM} } \right] = \left( {4;0;5} \right)\) làm vec tơ pháp tuyến.

Phương trình mặt phẳng \(\left( {ABCD} \right):4x - 5z - 20 = 0.\)

c) Đúng: Có \(S\left( {\dfrac{9}{2};0;\dfrac{9}{2}} \right)\), \(M\left( {\dfrac{5}{2};0;2} \right)\) \( \Rightarrow \overrightarrow {MS} \left( {2;0;\dfrac{5}{2}} \right)\).

Chiều dài kim đồng hồ: \(MS = \sqrt {{2^2} + {0^2} + {{\left( {\dfrac{5}{2}} \right)}^2}}  = \dfrac{{\sqrt {41} }}{2} \approx 3,2 = 32cm.\)

Ta có \(\overrightarrow {MS} \left( {2;0;\dfrac{5}{2}} \right)\), \(\overrightarrow {{n_1}} \left( {4;0;5} \right)\), suy ra \(2\overrightarrow {MS}  = \overrightarrow {{n_1}}  \Rightarrow \overrightarrow {MS} \parallel \overrightarrow {{n_1}} \).

Vậy \(MS \bot (ABCD)\).

d)  Sai: Mặt phẳng \(Oxy\) có vectơ pháp tuyến là \(\overrightarrow {{n_2}} (0;0;1)\), \(\left| {\overrightarrow {{n_2}} } \right| = 1\)

Có \(\overrightarrow {{n_1}} \left( {4;0;5} \right) \Rightarrow \left| {\overrightarrow {{n_1}} } \right| = \sqrt {{4^2} + {5^2}}  = \sqrt {41} \).

Góc tạo bởi mặt đồng hồ và mặt đất là \(\alpha \), có

\(\cos \alpha  = \dfrac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \dfrac{5}{{\sqrt {41} }} \Rightarrow \alpha  \approx 38,6{6^o}\)

\( \Rightarrow \beta  = {90^o} - \alpha  \approx 51,{34^o}\).

Vậy vĩ độ nơi đặt đồng hồ là \(51,{34^o}\).

Đáp án cần chọn là: S; S; Đ; S

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn