1) Tìm tất cả các cặp số nguyên $(x;y)$ thoả mãn $x^{2} + 10y^{2} - 6xy + y = 6$.2) Một mảnh đất
1) Tìm tất cả các cặp số nguyên $(x;y)$ thoả mãn $x^{2} + 10y^{2} - 6xy + y = 6$.
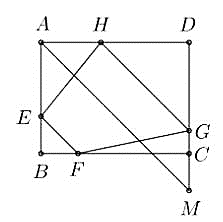
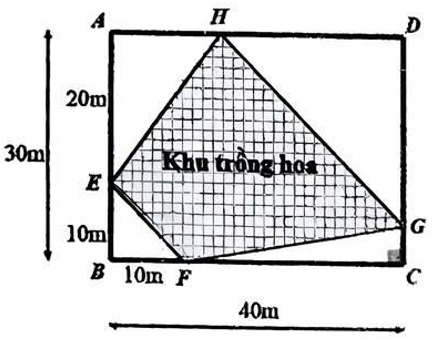
2) Một mảnh đất hình chữ nhật ABCD có $AB = 30~\text{m}$, $BC = 40~\text{m}$, có hai vị trí E,F cố định lần lượt thuộc cạnh AB và BC sao cho $BE = BF = 10~\text{m}$. Người ta tạo ra một khu đất hình thang $EFGH(EF//GH)$ để trồng hoa, trong đó các điểm G,H tương ứng thuộc các cạnh CD và AD. Hỏi diện tích lớn nhất của khu đất trồng hoa là bao nhiêu mét vuông?
Quảng cáo
1) Từ phương trình ban đầu tách thành $\left( {x - 3y} \right)^{2} + \left( {y - 2} \right)\left( {y + 3} \right) = 0$.
Do $x,y \in {\mathbb{Z}}$ và $\left( {x - 3y} \right)^{2} \geq 0\,\,\forall x,y$ nên suy ra $\left( {y - 2} \right)\left( {y + 3} \right) \leq 0$
TH1: $y - 2 \geq 0$ và $y + 3 \leq 0$. Vô lý
TH2: $y - 2 \leq 0$ và $y + 3 \geq 0$ suy ra $- 3 \leq y \leq 2$
Xét tiếp các khả năng xảy ra.
2)
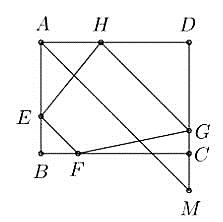
Gọi độ dài $AH = x$ với $0 < x < 40$ (m). Khi đó $HD = 40 - x$ (m)
Qua $A$ kẻ đường thẳng song song với $EF$ cắt $DC$ tại $M$
Ta cần tìm giá trị nhỏ nhất của $P = 10x + \dfrac{\left( {40 - x} \right)^{2}}{2} + 15\left( {x - 10} \right)$
1) $x^{2} + 10y^{2} - 6xy + y = 6$
$x^{2} - 6xy + 9y^{2} + y^{2} + y - 6 = 0$
$\left( {x - 3y} \right)^{2} + \left( {y - 2} \right)\left( {y + 3} \right) = 0$
Do $x,y \in {\mathbb{Z}}$ và $\left( {x - 3y} \right)^{2} \geq 0\,\,\forall x,y$ nên suy ra $\left( {y - 2} \right)\left( {y + 3} \right) \leq 0$
TH1: $y - 2 \geq 0$ và $y + 3 \leq 0$. Vô lý
TH2: $y - 2 \leq 0$ và $y + 3 \geq 0$ suy ra $- 3 \leq y \leq 2$
Vậy $y \in \left\{ {- 3, - 2, - 1,0,1,2} \right\}$
Với $y = - 3$ ta có $\left( {x + 9} \right)^{2} = 0$ suy ra $x = - 9$ (tm)
Với $y = - 2$ ta có $\left( {x + 6} \right)^{2} - 4 = 0$ suy ra $x = - 4$ (tm); $x = - 8$ (tm)
Với $y = - 1$ ta có $\left( {x + 3} \right)^{2} - 6 = 0$ không có nghiệm nguyên x
Với $y = 0$ ta có $x^{2} - 6 = 0$ không có nghiệm nguyên x
Với $y = 1$ ta có $\left( {x - 3} \right)^{2} - 4 = 0$ suy ra $x = 5$ (tm); $x = 1$ (tm)
Với $y = 2$ ta có $\left( {x - 6} \right)^{2} = 0$ suy ra $x = 6$ (tm)
Vậy các cặp nghiệm nguyên là $\left( {- 9, - 3} \right);\left( {- 4, - 2} \right);\left( {- 8, - 2} \right);\left( {5,1} \right);\left( {1,1} \right);\left( {6,2} \right)$
Vậy có tất cả 6 cặp nghiệm nguyên $(x;y)$
2)
Gọi độ dài $AH = x$ với $0 < x < 40$ (m). Khi đó $HD = 40 - x$ (m)
Qua $A$ kẻ đường thẳng song song với $EF$ cắt $DC$ tại $M$
Khi đó $\angle DHG = \angle DAM = \angle BEF = 45{^\circ}$
Do đó tam giác $DHG$ vuông cân tại $D$
Suy ra $DG = DH = 40 - x$ (m)
Như vậy $GC = DC - DG = 30 - \left( {40 - x} \right) = x - 10\,\,(m)$
Ta có:
$S_{AHE} = \dfrac{1}{2}AH.AE = \dfrac{1}{2}.20.x = 10x\,\,\left( m^{2} \right)$
$S_{DHG} = \dfrac{1}{2}DH.DG = \dfrac{1}{2}.\left( {40 - x} \right)^{2}\,\,\left( m^{2} \right)$
$S_{FCG} = \dfrac{1}{2}CG.CF = \dfrac{1}{2}.\left( {x - 10} \right).30 = 15\left( {x - 10} \right)\,\,\left( m^{2} \right)$
$S_{EFGH} = S_{ABCD} - \left( {S_{EBF} + S_{AEH} + S_{HDG} + S_{FGC}} \right)$
Đặt $P = S_{AEH} + S_{HDG} + S_{FGC}$
Ta cần tìm giá trị nhỏ nhất của $P = 10x + \dfrac{\left( {40 - x} \right)^{2}}{2} + 15\left( {x - 10} \right)$
$P = 10x + \dfrac{x^{2} - 80x + 1600}{2} + 15x - 150$
$P = \dfrac{x^{2}}{2} - 15x + 650$
$2P = x^{2} - 30x + 1300$
$2P = \left( {x - 15} \right)^{2} + 1075 \geq 1075,\,\,\forall 0 < x < 40$
Do đó $P \geq 537,5$
Vậy diện tích lớn nhất của mảnh đất trồng hoa là $30.40 - \dfrac{1}{2}.10^{2} - 537,5 = 612,5\,\,\left( m^{2} \right)$
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
