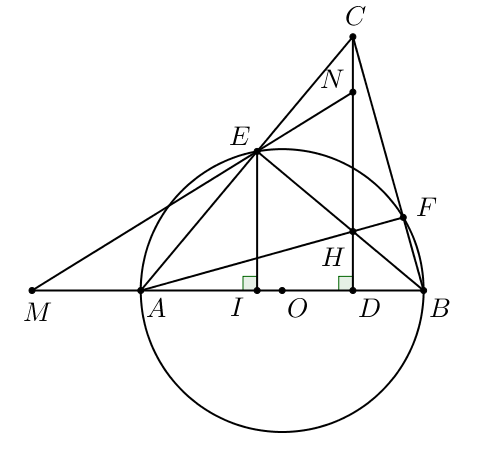
1. Một thùng nhựa dạng hình trụ có bán kính đáy 10 cm và chiều cao 30 cm.a) Tính thể tích của
1. Một thùng nhựa dạng hình trụ có bán kính đáy 10 cm và chiều cao 30 cm.
a) Tính thể tích của thùng nhựa.
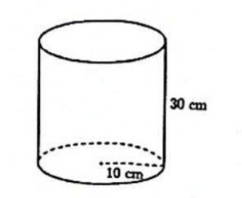
b) Bác Hoa mua một thúng muối vun đầy, cái thúng có dạng nửa hình cầu với đường kính 48 cm, phần muối vun lên có dạng hình nón với chiều cao 14 cm (hình vẽ bên). Bác Hoa cần phải sử dụng ít nhất bao nhiêu thùng nhựa như trên để đựng hết lượng muối đã mua.
(Bỏ qua bề dày của thùng nhựa và thúng)
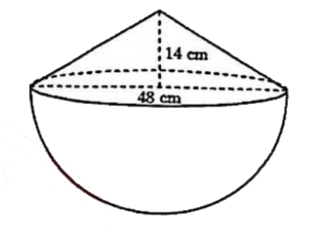
2. Cho đường tròn (O) đường kính AB bằng 2R. Gọi D là trung điểm của OB, vē đường thẳng a qua D và vuông góc với AB. Trên đường thẳng a, lấy điểm C nằm ngoài đường tròn (O). Hai đường thẳng AC, BC cắt đường tròn (O) lần lượt tại E, F (với E khác A và F khác B). Gọi H là giao điểm của AF và CD.
a) Chứng minh tứ giác BDHF nội tiếp.
b) Chứng minh $AE \cdot AC = 3R^{2}$.
c) Vẽ EI vuông góc với AB tại I, cho biết $EI = 8~\text{cm}$ và $R = 10~\text{cm}$. Đường thẳng qua E cắt hai tia DA, DC lần lượt tại M, N. Đặt $IM = x~\text{cm}$, tính DN theo x và tìm x để diện tích tam giác DMN nhỏ nhất.
Quảng cáo
1) a) Thể tích của thùng nhựa: $V = \pi R^{2}h$
b) Tính thể tích muối = Thể tích thúng muối + Thể tích phần muối vun lên.
Từ đó xác định số thùng nhựa cần để chứa hết muối = Thể tích muối : Thể tích thùng nhựa.
2) a) Chứng minh B, D, H, F cùng thuộc đường tròn đường kính BH hay tứ giác BDHF nội tiếp.
b) Chứng minh $\Delta AEB \sim \Delta ADC\left( {g.g} \right)$
Suy ra $AE.AC = AD.AB$
Do D là trung điểm của OB nên $OD = \dfrac{1}{2}OB = \dfrac{1}{2}R$
Suy ra $AE.AC = AD.AB = \dfrac{3}{2}R.2R = 3R^{2}$
c) Chứng minh $\Delta AEI \sim \Delta EBI\left( {g.g} \right)$. Khi đó $IE^{2} = IA.IB$
Suy ra $IA.IB = 8^{2} = 64$
Mà $IA + IB = AB = 2.10 = 20$
Nên độ dài $IA,IB$ là nghiệm của phương trình $X^{2} - 20X + 64 = 0$
Giải phương trình ta được $X = 16$ và $X = 4$
Do $IM = x$ nên $MA = IM - IA = x - 4$ (cm)
Suy ra $MD = IM + ID = x + IB - DB = x + 16 - 5 = x + 11$ (cm)
Suy ra $\dfrac{8}{ND} = \dfrac{x}{x + 11}$ hay $ND = \dfrac{8\left( {x + 11} \right)}{x}$ (cm)
Khi đó diện tích tam giác DMN là $S = \dfrac{1}{2}DM.DN = \dfrac{1}{2}\left( {x + 11} \right).\dfrac{8\left( {x + 11} \right)}{x}$ cm2
1)
a) Thể tích của thùng nhựa: $V = \pi R^{2}h$
$V = \pi.10^{2}.30 = 3000.\pi\,\left( {cm^{3}} \right)$
b) Chia thúng muối thành hai phần:
Bán kính thúng là: $48:2 = 24\left( {cm} \right)$
Thể tích thúng muối là: $V_{1} = \dfrac{1}{2}.\dfrac{4}{3}\pi.R^{3} = \dfrac{1}{2}.\dfrac{4}{3}.\pi.(24)^{3} = 9216\pi\left( {cm^{3}} \right)$
Phần muối vun lên có thể tích là: $V_{2} = \dfrac{1}{3}\pi.R^{2}.h = \dfrac{1}{3}\pi.24^{2}.14 = 2688\pi\left( {cn^{3}} \right)$
Thể tích muối: $V = V_{1} + V_{2} = 9216\pi + 2688\pi = 11904\pi\left( {cm^{3}} \right)$
Số thùng nhựa cần để chứa hết muối là: $\dfrac{11904\pi}{3000\pi} = 3,968$
Vậy cần ít nhất 4 thùng mới đựng đủ số muối trên.
2)
a) Do $E,F \in (O)$ nên $\angle AEB = \angle AFB = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)
Khi đó $\Delta BHF$ vuông tại F nên B, F, H cùng thuộc đường tròn đường kính BH
Và $\Delta HDB$ vuông tại D nên H, D, B cùng thuộc đường tròn đường kính BH
Vậy B, D, H, F cùng thuộc đường tròn đường kính BH hay tứ giác BDHF nội tiếp.
b) Xét $\Delta AEB$ và $\Delta ADC$ có
$\angle DAC$ là góc chung
$\angle AEB = \angle ADC\left( {= 90^{0}} \right)$
Suy ra $\Delta AEB \sim \Delta ADC\left( {g.g} \right)$
Suy ra $\dfrac{AE}{AD} = \dfrac{AB}{AC}$ hay $AE.AC = AD.AB$
Do D là trung điểm của OB nên $OD = \dfrac{1}{2}OB = \dfrac{1}{2}R$ suy ra
$AD = OA + OD = R + \dfrac{1}{2}R = \dfrac{3}{2}R$
Suy ra $AE.AC = AD.AB = \dfrac{3}{2}R.2R = 3R^{2}$
c) Ta có $\angle EAI = \angle IEB$ (do cùng cộng với $\angle AEI$ bằng $90^{0}$)
Suy ra $\Delta AEI \sim \Delta EBI\left( {g.g} \right)$. Khi đó $\dfrac{IE}{IB} = \dfrac{IA}{IE}$ hay $IE^{2} = IA.IB$
Suy ra $IA.IB = 8^{2} = 64$
Mà $IA + IB = AB = 2.10 = 20$
Nên độ dài $IA,IB$ là nghiệm của phương trình $X^{2} - 20X + 64 = 0$
Giải phương trình ta được $X = 16$ và $X = 4$
Vậy $IA = 4$ cm và $IB = 16$cm (Do $IA < IB$)
Do $IM = x$ nên $MA = IM - IA = x - 4$ (cm)
Suy ra $MD = IM + ID = x + IB - DB = x + 16 - 5 = x + 11$ (cm)
Ta có $EI \parallel DN$ (do cùng vuông góc với AB) nên $\dfrac{MI}{MD} = \dfrac{EI}{ND}$
Suy ra $\dfrac{8}{ND} = \dfrac{x}{x + 11}$ hay $ND = \dfrac{8\left( {x + 11} \right)}{x}$ (cm)
Khi đó diện tích tam giác DMN là
$S = \dfrac{1}{2}DM.DN = \dfrac{1}{2}\left( {x + 11} \right).\dfrac{8\left( {x + 11} \right)}{x} = 4.\dfrac{\left( {x + 11} \right)^{2}}{x}$ cm2
Ta có
$\dfrac{4\left( {x + 11} \right)^{2}}{x} = 4.\dfrac{x^{2} + 22x + 121}{x} = 4.\left( {x + \dfrac{121}{x} + 22} \right) \geq 4.\left\lbrack {2\sqrt{x.\dfrac{121}{x}} + 22} \right\rbrack = 176$ (Áp dụng bất đẳng thức Cauchy). Dấu bằng có khi $x = \dfrac{121}{x}$ hay $x = 11$
Vậy $x = 11$ thì diện tích tam giác DMN nhỏ nhất
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
