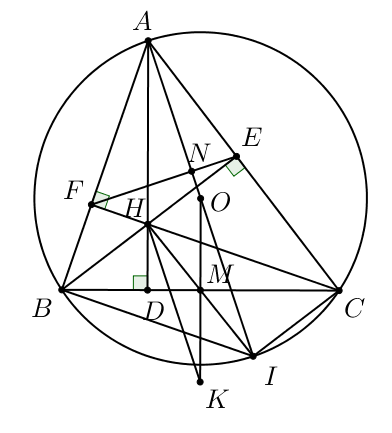
1) Nước ta có rất nhiều trò chơi dân gian, trong đó có trò chơi đánh đu. Khi người chơi nhún
1) Nước ta có rất nhiều trò chơi dân gian, trong đó có trò chơi đánh đu. Khi người chơi nhún đều, dây đu sẽ đưa người chơi dao động quanh vị trí cân bằng $A_{o}$. Trong hình minh họa bên, người chơi đang ở vị trí $A$ với $OA = 5\, cm$ và dây $OA$ tạo với phương thẳng đứng $OA_{o}$ một góc $\alpha = 30^{o}.$Tính độ dài đoạn thẳng $AB$ là khoảng cách từ vị trí $A$ đến đường thẳng $OA_{o}$.
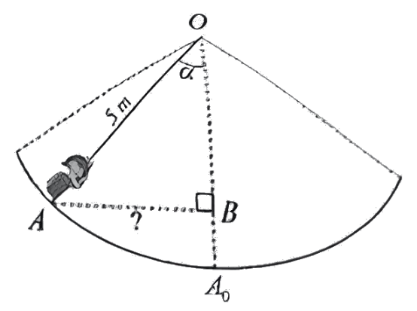
2) Cho tam giác $ABC$ nhọn nội tiếp đường tròn $(O)$, các đường cao $AD,BE,CF$ của tam giác $ABC$ (với $D \in BC,E \in AC,F \in AB$) cắt nhau tại $H$.
a) Chứng minh tứ giác $BFEC$ nội tiếp đường tròn.
b) Chứng minh $AE.AC = AF.AB$
c) Gọi $K$ là điểm đối xứng với điểm $O$ qua đường thẳng $BC$. Chứng minh $HK\bot EF$.
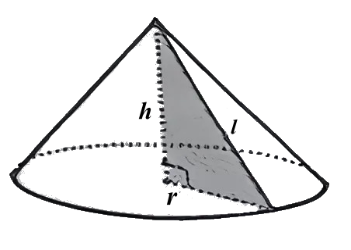
3) Chiếc nón lá do một làng nghề ở Huế làm thủ công là hình nón có chiều cao bằng $19\, cm$, đường kính đáy bằng $40\, cm$. Người ta dùng hai lớp lá để phủ lên bề mặt xung quanh của nón (tham khảo hình vẽ). Tính diện tích lá cần dùng để làm một chiếc nón (bỏ qua mọi hao hụt khi làm nón; lấy $\pi = 3,14$; kết quả làm tròn đến hàng đơn vị; cho $S = \pi rl,\,\, V = \dfrac{1}{3}\pi r^{2},\,\, l^{2} = r^{2} + h^{2}$).
Quảng cáo
1) Áp dụng tỉ số lượng giác của góc nhọn.
2)
a) Chứng minh $\Delta BEC$ vuông tại E và $\Delta BFC$ vuông tại F
Suy ra B, C, E, F cùng thuộc đường tròn đường kính BC hay BFEC nội tiếp đường tròn.
b) Chứng minh $\Delta AEF \sim \Delta ABC\left( {g.g} \right)$
Suy ra $\dfrac{AE}{AB} = \dfrac{AF}{AC}$ hay $AE.AC = AF.AB$.
c) Gọi N là giao điểm của AO và EF, gọi M là giao điểm của BC và OK.
Do K đối xứng với O qua BC nên BC là trung trực của OK hay $BC\bot OK$ tại M
Chứng minh $BHCI$ là hình bình hành
Chứng minh $HK \parallel AO$ (1) và $AO\bot EF$ (2)
Từ (1) và (2) suy ra $HK\bot EF$
3) Áp dụng $S_{xq} = \pi rl$
1) Ta có $\Delta OAB$ vuông tại B nên ta có $\sin\alpha = \dfrac{AB}{OA}$ suy ra $AB = OA.\sin\alpha = 5.\sin 30^{0} = 2,5$ (m)
Vậy độ dài của đoạn AB bằng 2,5 m.
2)
a) Do BE, CF là đường cao nên $\Delta BEC$ vuông tại E và $\Delta BFC$ vuông tại F
$\Delta BEC$ vuông tại E nên B, E, C cùng thuộc đường tròn đường kính BC
$\Delta BFC$ vuông tại F nên B, F, C cùng thuộc đường tròn đường kính BC
Suy ra B, C, E, F cùng thuộc đường tròn đường kính BC hay BFEC nội tiếp đường tròn.
b) Do BFEC nội tiếp đường tròn nên $\angle ACB + \angle BFE = 180^{0}$ (tính chất)
Mà $\angle AFE + \angle BFE = 180^{0}$ (hai góc kề bù) nên $\angle ACB = \angle AFE$
Xét $\Delta AEF$ và $\Delta ACB$ có $\angle ACB = \angle AFE$ và $\angle BAC$ chung
Suy ra $\Delta AEF \sim \Delta ABC\left( {g.g} \right)$
Suy ra $\dfrac{AE}{AB} = \dfrac{AF}{AC}$ hay $AE.AC = AF.AB$.
c) Gọi N là giao điểm của AO và EF, gọi M là giao điểm của BC và OK.
Do K đối xứng với O qua BC nên BC là trung trực của OK hay $BC\bot OK$ tại M
Ta có $OB = OC$ (cùng bằng bán kính) nên $\Delta OBC$ cân tại O
Mà OM là đường cao nên OM đồng thời là trung tuyến hay M là trung điểm của BC
Kẻ đường kính AI của (O). Khi đó $\angle ACI = \angle ABI = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)
Suy ra $CI \parallel BE$ (cùng vuông góc với AC) và $BI \parallel CH$ (do cùng vuông góc với AB)
Suy ra $BHCI$ là hình bình hành
Mà M là trung điểm của BC nên M là trung điểm của HI
Xét $\Delta AHI$ có M là trung điểm của HI và O là trung điểm của AI nên OM là đường trung bình của $\Delta AHI$
Suy ra $AH = 2OM$ và $AH \parallel OM$
Mà $OK = 2OM$ nên suy ra $AH = OK$ và $AH \parallel OK$
Suy ra $AHMO$ là hình bình hành nên $HK \parallel AO$ (1)
Ta có $\angle FAN + \angle AFN = \angle BCI + \angle ACB = \angle ACI = 90^{0}$
Suy ra $\Delta ANF$ vuông tại N hay $AO\bot EF$ (2)
Từ (1) và (2) suy ra $HK\bot EF$
3) Đường kính đáy hình nón bằng 40cm nên có bán kính là 20cm
Độ dài đường sinh của hình nón là là $l = \sqrt{r^{2} + h^{2}} = \sqrt{20^{2} + 19^{2}} = \sqrt{761}$ cm
Khi đó diện tích xung quanh của hình nón là $S_{xq} = \pi rl = 3,14.20.\sqrt{761} \approx 1732,415$ cm2
Vậy diện tích lá cần dùng để làm nón là $2.1732,415 \approx 3465$ cm2.
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
