Một lượng khí He chứa trong một xilanh đậy kín bởi một pit-tông biến đổi

Câu hỏi số 806346:

Vận dụng

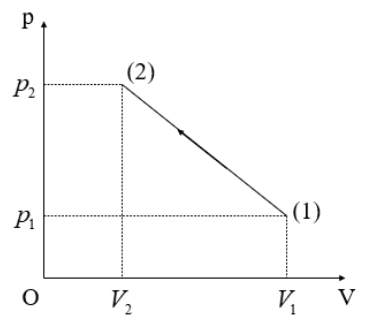
Một lượng khí He chứa trong một xilanh đậy kín bởi một pit-tông biến đổi chậm từ trạng thái (1) đến trạng thái (2) theo đồ thị (hình bên). Biết rằng ở trạng thái (1) khí có thể tích 30 lít và áp suất 5 atm, ở trạng thái (2) khí có thể tích là 10 lít và và áp suất 15 atm. Tỉ số giữa động năng trung bình cực đại và cực tiểu của các phân tử khí trong quá trình trên là bao nhiêu (làm tròn kết quả đến chữ số hàng phần mười)?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:806346

Phương pháp giải

Phương trình trạng thái của khí lí tưởng: $\dfrac{pV}{T} = const$

Động năng trung bình của phân tử khí: $\overline{W_{d}} = \dfrac{3}{2}kT$

Giải chi tiết

Ta có phương trình trạng thái:

$\left. \dfrac{pV}{T} = const\Rightarrow\left( {pV} \right) \sim T \right.$

Mặt khác: ${W_d} \sim T \Rightarrow {W_d} \sim \left( {pV} \right)$

Từ đồ thị ta thấy quá trình biến đổi từ trạng thái (1) → (2) là đoạn thẳng, sự phụ thuộc của áp suất vào thể tích được biểu diễn bởi phương trình:

$p = {p_2} + a.\left( {V - {V_2}} \right)$

Với a là hệ số

Tại trạng thái (1) có:

$\begin{array}{l}{p_1} = {p_2} + a.\left( {{V_1} - {V_2}} \right)\\ \Rightarrow 5 = 15 + a.\left( {30 - 10} \right)\\ \Rightarrow a = - 0,5\,\,\left( {atm/lit} \right)\\ \Rightarrow p = 15 - 0,5.\left( {V - 10} \right) = - 0,5V + 20\end{array}$

Ta có phương trình Clapeyron:

$pV = nRT = \dfrac{m}{\mu }.RT \Rightarrow T = \dfrac{{\mu pV}}{{mR}}$

Nhiệt độ của khí cao nhất:

${T_{\max }} \Leftrightarrow \left( {pV} \right)\max $

Ta có:

$\begin{array}{l}
pV = \left( { - 0,5V + 20} \right).V = - 0,5{V^2} + 20V\\
\Rightarrow pV = - 0,5{\left( {V - 20} \right)^2} + 200 \Rightarrow \left( {pV} \right)\max = 200
\end{array}$

Nhiệt độ của khí thấp nhất:

${T_{\min }} \Leftrightarrow \left( {pV} \right)\min $

Đặt: $y = pV = \left( { - 0,5V + 20} \right).V = - 0,5{V^2} + 20V$

Đồ thị hàm số y(V) là parabol có bề lõm hướng xuống, nên ymin tại biên của V:

$\left( {pV} \right)\min = {p_1}{V_1} = {p_2}{V_2} = 150$

Ta có tỉ số:

$ \Rightarrow \dfrac{{{W_{d\max }}}}{{{W_{d\min }}}} = \dfrac{{{{\left( {pV} \right)}_{\max }}}}{{{{\left( {pV} \right)}_{\min }}}} = \frac{{200}}{{150}} \approx 1,3$

Đáp án cần điền là: 1,3

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.