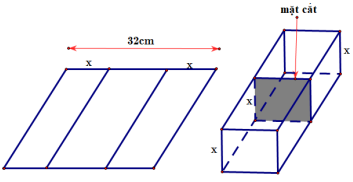
Một người muốn uốn tấm tôn phẳng hình chữ nhật có bề ngang 32 cm , thành một rãnh dẫn

Câu hỏi số 811656:

Vận dụng

Một người muốn uốn tấm tôn phẳng hình chữ nhật có bề ngang 32 cm , thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông như hình vẽ. Biết rằng diện tích mặt cắt ngang của rãnh nước phải lớn hơn hoặc bằng $120~\text{cm}^{2}$. Hỏi độ cao tối thiểu và tối đa của rãnh dẫn nước là bao nhiêu cm?

Quảng cáo

Xem lời giải

Câu hỏi:811656

Phương pháp giải

Lập hàm số biểu diễn diện tích mặt cắt ngang rãnh dẫn nước.

Giải bất phương trình $S \geq 0$.

Giải chi tiết

Bề ngang còn lại của tấm tôn sau khi gập thành rãnh dẫn nước: $32 - 2x(~\text{cm})$.

Diện tích mặt cắt ngang rãnh dẫn nước: $S = x(32 - 2x) = - 2x^{2} + 32x$.

Theo giả thiết:

$\left. S \geq 120\Leftrightarrow - 2x^{2} + 32x \geq 120\Leftrightarrow - 2x^{2} + 32x - 120 \geq 0 \right.$.

Ta có: $\left. - 2x^{2} + 32x - 120 \geq 0\Leftrightarrow x \in \lbrack 6;10\rbrack \right.$.

Vậy rãnh dẫn nước chỉ đạt yêu cầu khi độ cao tối thiểu và tối đa của nó lần lượt bằng 6 cm và 10 cm.

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10