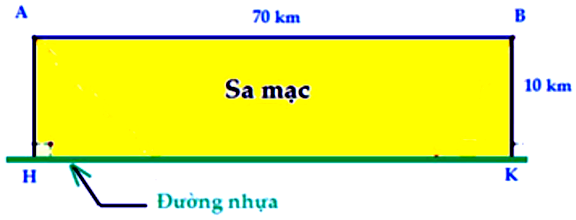
Một người đang ở tại điểm $A$ trên sa mạc. Ông ta muốn đến điểm $B$ và cách $A$ một

Câu hỏi số 822108:

Vận dụng

Một người đang ở tại điểm $A$ trên sa mạc. Ông ta muốn đến điểm $B$ và cách $A$ một đoạn là 70 $km$. Trong sa mạc thì xe ông ta chỉ có thể di chuyển với vận tốc $30km/h$. Ông ấy phải đến được điểm $B$ trong 2 giờ. Biết rằng có một con đường nhựa $HK$ song song với $AB$ và cách $AB$ một đoạn 10 km. Trên đường nhựa này thì xe ông ấy có thể di chuyển với vận tốc $50\text{km}/\text{h}$. Để đến $B$ sớm nhất ( đảm bảo trong khung giờ cho phép) thì ông phải đi theo con đường nào?

Quảng cáo

Xem lời giải

Câu hỏi:822108

Phương pháp giải

Gọi C, D là 2 điểm trên HK. Khi đó ta chia quãng đường thành $\left. A\rightarrow C\rightarrow D\rightarrow B \right.$

Gọi $HC = x(0 < x < 70);DK = y(0 < y < 70);$

Tính thời gian đi AC, CD, DB để từ đó tính thời gian từ AB

Khi đó $t_{AB} = f\left( {x,y} \right) = f(x) + f(y)$ từ đó tìm GTNN của từng $f(x);f(y)$.

Giải chi tiết

Thời gian nếu đi trực tiếp từ $A$ đến B trên sa mạc là $\dfrac{70}{30} = \dfrac{7}{3} > 2$

Do đó, nhà địa chất học không thể đến đúng thời gian quy định.

Vì vậy cần thiết phải chia quãng đường đi được thành 3 giai đoạn: $\left. A\rightarrow C\rightarrow D\rightarrow B \right.$

Đặt $HC = x(0 < x < 70);DK = y(0 < y < 70);$

Thời gian đi từ $\left. A\rightarrow C \right.$ là $\dfrac{\sqrt{10^{2} + x^{2}}}{30}$

Thời gian đi từ $\left. C\rightarrow D \right.$ là $\dfrac{70 - \left( {x + y} \right)}{50}$

Thời gian đi từ $\left. D\rightarrow B \right.$ là $\dfrac{\sqrt{10^{2} + y^{2}}}{30}$

Tô̂ng thời gian đi từ $\left. A\rightarrow B \right.$ theo cách này là

$\dfrac{\sqrt{10^{2} + x^{2}}}{30} + \dfrac{70 - \left( {x + y} \right)}{50} + \dfrac{\sqrt{10^{2} + y^{2}}}{30}$ $= \dfrac{\sqrt{10^{2} + x^{2}}}{30} + \dfrac{35 - x}{50} + \dfrac{\sqrt{10^{2} + y^{2}}}{30} + \dfrac{35 - y}{50} = f(x) + f(y)$

Xét $f(u) = \dfrac{\sqrt{10^{2} + u^{2}}}{30} + \dfrac{35 - u}{50},0 < u < 70$

$\left. \Rightarrow f'(u) = \dfrac{u}{30\sqrt{10^{2} + u^{2}}} - \dfrac{1}{50} \right.$

$\left. f'(u) = 0\Leftrightarrow u = \dfrac{15}{2} \right.$

Lập bảng biến thiên ta được $\underset{u \in {({0;70})}}{\text{min}}f(u) = f\left( \dfrac{15}{2} \right) = \dfrac{29}{30}$

Khi đó $f(x) + f(y) \geq \dfrac{29}{30} + \dfrac{29}{30} \approx 1,93$

Dấu "$=$" xảy ra khi $x = y = \dfrac{15}{2}$.

Vậy để đến B sớm nhất thì ông ta phải đi trên đoạn $AC = 12,5km$, đoạn $CD = 55~km$; $DB = 12,5~km$.

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.