Hình vẽ bên dưới là hai bánh răng của một động cơ, chúng có

Câu hỏi số 836607:

Vận dụng

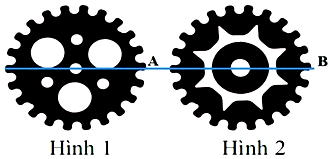
Hình vẽ bên dưới là hai bánh răng của một động cơ, chúng có cùng kích thước. Khi động cơ hoạt động, hai bánh răng quay đều, cùng chiều. Biết tốc độ quay của bánh răng ở hình 2 gấp ba tốc độ quay của bánh răng ở hình 1 và phương trình biểu thị độ cao của điểm $A$ ở bánh răng thứ nhất là $h = 2R + R\text{sin}\left( {\dfrac{\pi}{5}t} \right)$ (trong đó $R$ là bán kính bánh răng, $t$ là thời gian tính bằng phút, $h$ là độ cao của điểm $A$). Giả sử tại thời điểm bắt đầu khởi động, hai điểm $A,B$ có độ cao bằng nhau và tâm của hai bánh răng $O_{1},O_{2}$ ở độ cao $2R$ so với mặt đất. Tìm thời điểm đầu tiên sau khi động cơ hoạt động hai điểm $A,B$ có độ cao bằng nhau. Nhập kết quả dưới dạng phân số a/b.

Đáp án:

Đáp án đúng là: 5/4

Quảng cáo

Xem lời giải

Câu hỏi:836607

Phương pháp giải

Vì hai bánh răng có cùng kích thước, tốc độ của bánh răng thứ hai gấp ba tốc độ của bánh răng thứ nhất và tại thời điểm ban đầu, hai điểm $A,B$ có độ cao bằng nhau nên phương trình biểu thị độ cao của điểm $B$ là $h' = 2R + R\text{sin}\left( {\dfrac{3\pi}{5}t} \right)$.

Hai điểm $A,B$ có độ cao bằng nhau khi $h = h'$. Giải phương trình tìm nghiệm t nguyên dương nhỏ nhất.

Giải chi tiết

Hai điểm $A,B$ có độ cao bằng nhau khi $h = h'$. Ta có phương trình:

$\left. 2R + R\text{sin}\left( {\dfrac{\pi}{5}t} \right) = 2R + R\text{sin}\left( {\dfrac{3\pi}{5}t} \right)\Leftrightarrow\text{sin}\left( {\dfrac{\pi}{5}t} \right) = \text{sin}\left( {\dfrac{3\pi}{5}t} \right)\Leftrightarrow\left\lbrack \begin{array}{l} {\dfrac{3\pi}{5}t = \dfrac{\pi}{5}t + k2\pi} \\ {\dfrac{3\pi}{5}t = \pi - \dfrac{\pi}{5}t + k2\pi} \end{array} \right. \right.$

$\left. \Leftrightarrow\left\lbrack \begin{array}{l} {2\pi t = k10\pi} \\ {4\pi t = 5\pi + k10\pi} \end{array}\Leftrightarrow\left\lbrack {\begin{array}{l} {t = 5k} \\ {t = \dfrac{5}{4} + \dfrac{5}{2}k} \end{array}\left( {k \in {\mathbb{Z}}} \right)} \right. \right. \right.$.

Họ nghiệm thứ nhất có nghiệm dương nhỏ nhất là $t = 5$.

Họ nghiệm thứ hai có nghiệm dương nhỏ nhất là $t = \dfrac{5}{4}$.

Vậy thời điểm đầu tiên sau khi động cơ hoạt động, hai điểm $A,B$ có độ cao bằng nhau là $t = \dfrac{5}{4}$ phút.

Đáp án cần điền là: 5/4

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.