(2,5 điểm)a) Cho biểu thức $A = \sqrt{2x - 5}$. Tìm điều kiện xác định của biểu thức $A$.b)

Câu hỏi số 848576:

Thông hiểu

(2,5 điểm)

a) Cho biểu thức $A = \sqrt{2x - 5}$. Tìm điều kiện xác định của biểu thức $A$.

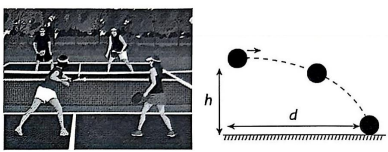
b) Pickleball là một môn thể thao thi đấu trong nhà hoặc ngoài trời, theo hai thể thức chính là đấu đơn (hai người chơi), hoặc đấu đôi (bốn người chơi) trên sân hình chữ nhật. Người chơi dùng một chiếc vợt mặt nhẵn (vợt phẳng) để đánh một quả bóng nhựa rỗng, có đục lỗ, qua lưới cao 0,86 m cho đến khi một bên không thể trả bóng hoặc phạm luật. (Nguồn: Wikipedia)

Giả sử một quả bóng pickleball khi được đánh theo phương ngang với tốc độ $v$ (m/s) tại độ cao $h$ (m) so với mặt đất sẽ dịch chuyển theo phương ngang một quãng đường $d$ (m) cho đến khi chạm đất được cho bởi công thức sau: $d = v\sqrt{\dfrac{h}{4,9}}$. Hỏi quả bóng pickleball đi được bao xa theo phương ngang từ khi được đánh theo phương ngang với tốc độ 14 m/s tại độ cao 0,9 m so với mặt đất.

c) Rút gọn biểu thức sau: $\dfrac{3}{\sqrt{7} - 2} + \sqrt{{(3 - \sqrt{7})}^{2}}$

Quảng cáo

Xem lời giải

Câu hỏi:848576

Phương pháp giải

a) Căn thức bậc hai $\sqrt{P}$ xác định (có nghĩa) khi biểu thức dưới dấu căn không âm, tức là $P \geq 0$.

b) Thay trực tiếp các giá trị đã cho của v và h vào công thức, sau đó thực hiện các phép tính căn bậc hai và nhân chia số thập phân.

c) Thực hiện trục căn thức ở mẫu

Sử dụng hằng đẳng thức $\left. \sqrt{A^{2}} = \middle| A \right|$

Giải chi tiết

a) Để biểu thức A xác định, thì

$2x - 5 \geq 0$

$2x \geq 5$

$x \geq \dfrac{5}{2}$

Vậy điều kiện xác định của biểu thức A là $x \geq \dfrac{5}{2}$

b) Quãng đường quả bóng đi được theo phương ngang là: $d = 14.\sqrt{\dfrac{0,9}{4,9}} = 6$

Vậy quả bóng đi được 6 mét theo phương ngang cho đến khi chạm đất.

c) $\dfrac{3}{\sqrt{7} - 2} + \sqrt{{(3 - \sqrt{7})}^{2}}$

$= \dfrac{3(\sqrt{7} + 2)}{(\sqrt{7} - 2)(\sqrt{7} + 2)} + \left| {3 - \sqrt{7}} \right|$

$= \dfrac{3(\sqrt{7} + 2)}{7 - 4} + 3 - \sqrt{7}$

$\dfrac{3(\sqrt{7} + 2)}{3} + 3 - \sqrt{7}$

$= (\sqrt{7} + 2) + 3 - \sqrt{7}$

$= 5$

Vậy $\dfrac{3}{\sqrt{7} - 2} + \sqrt{{(3 - \sqrt{7})}^{2}} = 5$

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link