Một khung dây tròn cứng có bán kính R = 10 cm được giữ trong từ trường đều vuông góc với

Câu hỏi số 849119:

Thông hiểu

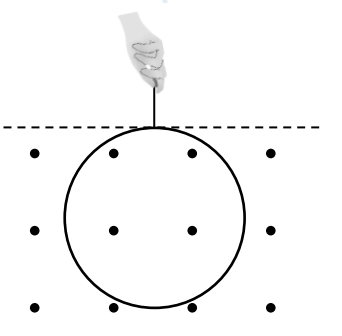
Một khung dây tròn cứng có bán kính R = 10 cm được giữ trong từ trường đều vuông góc với trang giấy và hướng ra ngoài. Dòng điện chạy qua khung dây có chiều ngược chiều kim đồng hồ và cường độ là I = 2 A. Ban đầu nó tiếp tuyến với ranh giới từ trường đều như hình vẽ. Bây giờ từ từ nâng khung dây theo phương thẳng đứng. Khi khung dây được nâng lên đoạn $\dfrac{2}{5}R$ thì lực căng dây là F = 0,01 N. Khi khung dây được nâng lên đoạn R thì lực căng dây là 1,16F. Bỏ qua từ trường do dòng điện gây ra. Độ lớn cảm ứng từ của từ trường là bao nhiêu Tesla. (kết quả làm tròn đến chữ số hàng phần trăm)?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:849119

Phương pháp giải

Phân tích lực tác dụng

Sử dụng lí thuyết về từ trường và chuyển động trong từ trường

Công thức tính các lực

Giải chi tiết

Do dòng điện chạy ngược chiều kim đồng hồ, cảm ứng từ $null$hướng ra ngoài mặt giấy nên lực từ tác dụng lên phần dây nằm trong từ trường có hướng xuống dưới.

Suy ra lực căng dây: $T = F_{t} + P$

trong đó:

$F_{t}$ là lực từ tác dụng lên khung dây,

$P$là trọng lượng khung dây.

Ta có: $F_{t} = BIl\sin\alpha$ $(\sin 90^{0} = 1)$

l là độ dài dây hình chiếu theo phương vuông góc thích hợp, và với biên là một đường thẳng ngang, ta có: _{$F_{t} = IB2x_{0}$} với _{$2x_{0}$} là độ dài dây cung cắt bởi đường biên.

Nếu gọi $h$là độ nâng lên so với vị trí ban đầu (ban đầu tiếp tuyến nên tâm cách biên $R$), thì tọa độ tâm so với biên là $- R + h$. Giao điểm với biên $y = 0$ cho:

_{$\begin{array}{l}
{x_{0} = \sqrt{R^{2} - {(R - h)}^{2}} = \sqrt{h(2R - h)}} \\
\left. \Rightarrow F_{\text{t}}(h) = 2IB\sqrt{h(2R - h)} \right.
\end{array}$}

Trường hợp 1: Nâng khung lên đoạn $\dfrac{2}{5}R$

_{$\begin{array}{l}
\left. h_{1} = \dfrac{2}{5}R = 0,04\Rightarrow\sqrt{h_{1}\left( {2R - h_{1}} \right)} = \sqrt{0,04 \cdot 0,16} = 0,08 \right. \\
{T_{1} = 0,01 = mg + 2IB(0,08) = mg + 0,16IB}
\end{array}$}

Trường hợp 2: Nâng khung lên đoạn R

_{$\begin{array}{l}
\left. h_{2} = R = 0,10\Rightarrow\sqrt{h_{2}\left( {2R - h_{2}} \right)} = \sqrt{0,1 \cdot 0,1} = 0,1 = R \right. \\
{T_{2} = 1,16T_{1} = 0,0116 = mg + 2IBR = mg + 0,2IB}
\end{array}$}

Lấy (2) - (1):

_{$\begin{array}{l}
\left. 0,0116 - 0,01 = (0,2 - 0,16)IB\Rightarrow 0,0016 = 0,04IB \right. \\
\left. IB = \dfrac{0,0016}{0,04} = 0,04\Rightarrow B = \dfrac{0,04}{I} = \dfrac{0,04}{2} = 0,02~\text{T} \right.
\end{array}$}

Đáp án cần điền là: 0,02

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.