Công tử Bạc Liêu có một mảnh đất hình vuông ở một khu đô

Câu hỏi số 860280:

Vận dụng

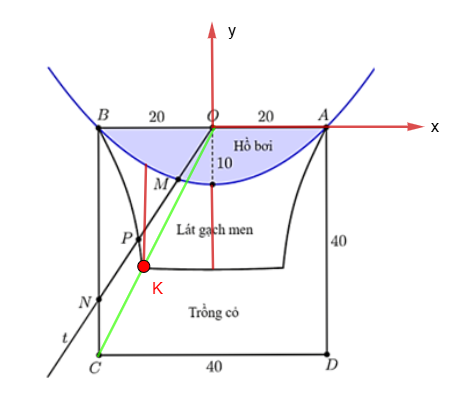
Công tử Bạc Liêu có một mảnh đất hình vuông ở một khu đô thị sầm uất, hình vuông có cạnh 40m, công tử dự định xây một hồ bơi được giới hạn bởi cạnh AB của hình vuông và một parabol đi qua hai đầu mút cạnh đó, đỉnh của parabol cách cạnh AB một đoạn 10m. Từ vị trí O là trung điểm AB, kẻ tia Ot bất kì cắt parabol và một cạnh khác của hình vuông theo thứ tự tại các điểm M, N. Gọi P là trung điểm MN, khi tia Ot quay quanh gốc O thì tập hợp các điểm P tạo thành đường cong $(L)$. Công tử dự định sử dụng một loại gạch men đặc biệt để lát nền cho toàn bộ khu vực được giới hạn bởi đường cong $(L)$ và parabol. Phần còn lại trên mảnh đất hình vuông đó thì công tử sẽ trồng cỏ.

Biết rằng chi phí xây hồ bơi là 5 triệu đồng $/\text{m}^{2}$, chi phí lát gạch men là 2 triệu đồng $/\text{m}^{2}$, chi phí trồng cỏ tự nhiên là 100 nghìn đồng/ $m^{2}$. Tính tổng số tiền mà công tử Bạc Liêu phải chi trả cho toàn bộ dự án trên theo đơn vị tỷ đồng (làm tròn đến hàng phần chục).

Trả lời:

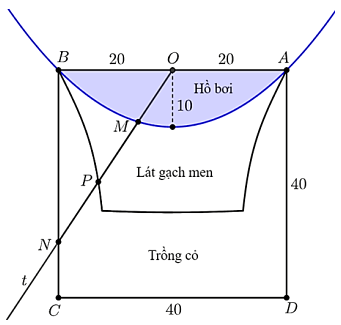
Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:860280

Phương pháp giải

Gọi $S_{1}$ là diện tích của hồ bơi, $S_{2}$ là diện tích của phần lát gạch men, $S_{3}$ là diện tích trồng cỏ.

Khi đó chi phí cho toàn bộ dự án là $T = 5.S_{1} + 2.S_{2} + 0,1.S_{3}$

Gắn hệ trục tọa độ Oxy.

Thiết lập hàm số của Parabol, hàm số $g(x)$ là quỹ đạo đi của điểm P (phương trình đường cong

(L))

Sử dụng ứng dụng của tích phân đề tính diện tích các hình phẳng.

Giải chi tiết

Gắn hệ trục tọa độ Oxy như hình vẽ, khi đó ta có $A(20;0)$; $B( - 20;0)$; $I(0; - 10)$, $C( - 20; - 40)$

Phương trình Parabol có dạng $y = ax^{2} + bx + c$ đi qua ba điểm A, B, I

Suy ra: $\left\{ \begin{matrix} {400a + 20b + c = 0} \\ {400a - 20b + c = 0} \\ {c = - 10} \end{matrix} \right.$ $\left. \Rightarrow\left\{ \begin{matrix} {a = \dfrac{1}{40}} \\ {b = 0} \\ {c = - 10} \end{matrix} \right. \right.$

$\left. \Rightarrow(P):y = \dfrac{1}{40}x^{2} - 10 \right.$.

Khi đó diện tích của hồ bơi là: $S_{1} = {\int_{- 20}^{20}\left| {\dfrac{1}{40}x^{2} - 10} \right|}\text{dx} = \dfrac{800}{3}\left( {~\text{m}^{2}} \right)$

Vì điểm $\left. M \in (P)\Rightarrow M\left( {x_{M},\dfrac{1}{40}x_{M}^{2} - 10} \right) \right.$.

Ta có điểm $N = \left( {- 20;y_{N}} \right)$.

Vì ba điểm O, M, N thẳng hàng, do đó

$\left. \overset{\rightarrow}{OM} = k\overset{\rightarrow}{ON}\Rightarrow\dfrac{x_{M}}{- 20} = \dfrac{\dfrac{x_{M}^{2}}{40} - 10}{y_{N}}\Rightarrow y_{N} = \dfrac{- x_{M}}{2} + \dfrac{200}{x_{M}} \right.$.

Vì $P$ là trung điểm của đoạn MN, suy ra

$\left. x_{P} = \dfrac{x_{M} + x_{N}}{2} = \dfrac{x_{M} - 20}{2}\Rightarrow x_{M} = 2x_{P} + 20 \right.$

$y_{P} = \dfrac{y_{M} + y_{N}}{2} = \dfrac{1}{2}\left( {\dfrac{x_{M}^{2}}{40} - 10 + \dfrac{- x_{M}}{2} + \dfrac{200}{x_{M}}} \right)$

$= \dfrac{1}{2}\left( {\dfrac{\left( {2x_{P} + 20} \right)^{2}}{40} - 10 - \dfrac{2x_{P} + 20}{2} + \dfrac{200}{2x_{P} + 20}} \right)$

$= \dfrac{1}{2}\left( {\dfrac{\left( {x_{P} + 10} \right)^{2}}{10} + \dfrac{100}{x_{P} + 10} - x_{P} - 20} \right)$

Suy ra điểm P thuộc đường cong có phương trình: $y = g(x) = \dfrac{1}{2}\left( {\dfrac{{(x + 10)}^{2}}{10} + \dfrac{100}{x + 10} - x - 20} \right)$.

Ta có phương trình đường thẳng $OC:y = 2x$.

Gọi K là giao điểm của đường thẳng OC với đồ thị hàm số $y = g(x)$.

Xét phương trình hoành độ giao điểm, ta có:

$\left. g(x) = 2x\Rightarrow\dfrac{1}{2}\left( {\dfrac{{(x + 10)}^{2}}{10} + \dfrac{100}{x + 10} - x - 20} \right) = 2x \right.$

$\left. \Rightarrow x_{K} \approx - 12,36 = \alpha \right.$

Tọa độ điểm K là $K(\alpha,2\alpha)$.

Khi đó diện tích phân được lát gạch men là:

$S_{2} = 2 \times \left( {{\int_{- 20}^{0}\dfrac{x^{2}}{40}} - 10 - g(x)dx + {\int_{a}^{0}\dfrac{x^{2}}{40}} - 10 - 2\alpha dx} \right) \approx 485,127 = \beta$

Suy ra diện tích trồng cỏ là:

$S_{3} = 40^{2} - S_{1} - S_{2} = 1600 - \dfrac{800}{3} - \beta = \gamma$.

Tổng số tiền phải chi trả cho dự án là:

$T = 5.\dfrac{800}{3} + 2.\beta + 0,1.\gamma \approx 2238,4085$(triệu đồng)$\approx 2,4$(tỉ đồng).

Đáp án cần điền là: 2,4

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.