Trong một triển lãm về nghệ thuật, bức tranh vẽ Monalisa có chiều cao 2m được treo trên tường
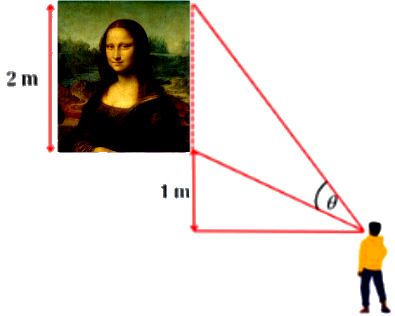
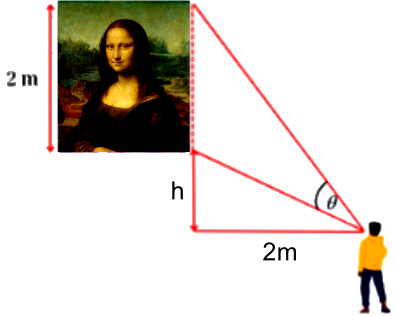
Trong một triển lãm về nghệ thuật, bức tranh vẽ Monalisa có chiều cao 2m được treo trên tường có mép dưới cao hơn tầm mắt người quan sát 1m (như hình vẽ).
Trả lời cho các câu 1, 2, 3 dưới đây:
Nếu người quan sát cách bức tranh 1m thì góc nhìn của người quan sát bằng bao nhiêu độ?
Đáp án đúng là: A
Tính góc bằng giá trị lượng giác tan
Khi $\left. NC = 2\Rightarrow\tan\angle ANC = \dfrac{3}{2}\Rightarrow\angle ANC = 56,31^{0} \right.$
$\left. \tan BNC = \dfrac{1}{2}\Rightarrow BNC = 26,565^{0} \right.$
Vậy góc quan sát $\theta = 56,31 - 26,565 = 29,74^{0}$
Đáp án cần chọn là: A
Người quan sát phải đứng cách tường bao nhiêu mét để có được tầm nhìn thuận lợi nhất? (tức là có góc nhìn θ lớn nhất)
Đáp án đúng là: A
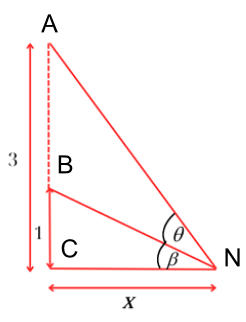
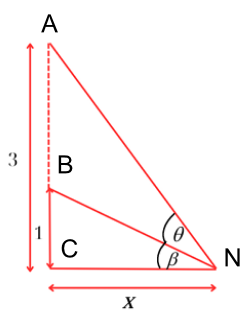
Gọi $\theta$là góc nhìn của người quan sát, $\beta$ là góc nghiêng của tia sáng truyền từ mép dưới bức ảnh tới mắt so với mặt đất, $\alpha = \theta + \beta$là góc nghiêng của tia sáng truyền từ mép trên bức ảnh tới so với mặt đất. Tính $\cot\theta$.
Gọi $\theta$ là góc nhìn của người quan sát, $\beta$là góc nghiêng của tia sáng truyền từ mép dưới bức ảnh tới mắt so với mặt đất, $\alpha = \theta + \beta$là góc nghiêng của tia sáng truyền từ mép trên bức ảnh tới so với mật đất.
Khi đó: $\cot\theta = \cot\left( {\alpha - \beta} \right) = \dfrac{1 + \cot\alpha.\cot\beta}{\cot\beta - \cot\alpha} = \dfrac{1 + \dfrac{x}{3}.\dfrac{x}{1}}{x - \dfrac{x}{3}} = \dfrac{x}{2} + \dfrac{3}{2x} \geq 2\sqrt{\dfrac{x}{2}.\dfrac{3}{2x}} = \sqrt{3}$
Vì hàm $\cot\theta$ luôn nghịch biến trên mỗi khoảng xác định nên $\theta$ càng lớn thì $\cot\theta$ càng nhỏ
Vậy để $\theta$ lớn nhất khi $\cot\theta$ nhỏ nhất hay $\cot\theta = \sqrt{3}$
Dấu bằng xảy ra khi và chỉ khi $x = \sqrt{3}.$
Đáp án cần chọn là: A
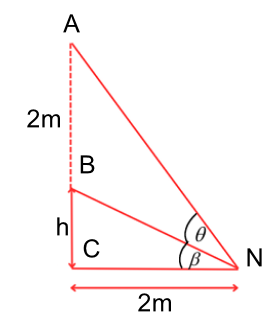
Giả sử người quan sát không thể thay đổi khoảng cách đứng cách bức tranh 2m, nhưng có thể điều chỉnh độ cao treo tranh. Để góc nhìn $\theta$ lớn nhất khi mép dưới của tranh cách tầm mắt một khoảng $h$. Khi đó góc $\theta$ bằng bao nhiêu?(Biết chiều cao tranh vẫn là $2\text{m}$).
Đáp án đúng là: C
Gọi $\theta$là góc nhìn của người quan sát, $\beta$ là góc nghiêng của tia sáng truyền từ mép dưới bức ảnh tới mắt so với mặt đất, $\alpha = \theta + \beta$là góc nghiêng của tia sáng truyền từ mép trên bức ảnh tới so với mặt đất. Tính $\cot\theta$ nhỏ nhất
Ta có $AB = NC = 2;BC = h$ khi đó
$\cot\theta = \cot\left( {\alpha - \beta} \right) = \dfrac{1 + \cot\alpha.\cot\beta}{\cot\beta - \cot\alpha} = \dfrac{1 + \dfrac{2}{h + 2}.\dfrac{2}{h}}{\dfrac{2}{h} - \dfrac{2}{h + 2}} = \dfrac{h^{2} + 2h + 4}{4}$
Xét $f(h) = \dfrac{h^{2} + 2h + 4}{4}$ với $h > 0$ có $f' = \dfrac{2h + 2}{4} > 0$ nên hàm số luôn đồng biến
Vậy $\min\cot\theta = f(0) = 1$ khi đó $\theta = 45^{0}$
Đáp án cần chọn là: C
Quảng cáo
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
