Cho parabol (P): \(y = {1 \over 3}{x^2}\) và đường thẳng (d): \(y = - x + 6\) a) Vẽ (P) và (d)
Cho parabol (P): \(y = {1 \over 3}{x^2}\) và đường thẳng (d): \(y = - x + 6\)
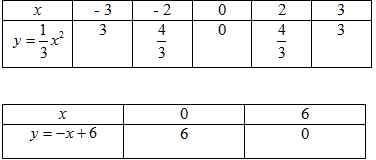
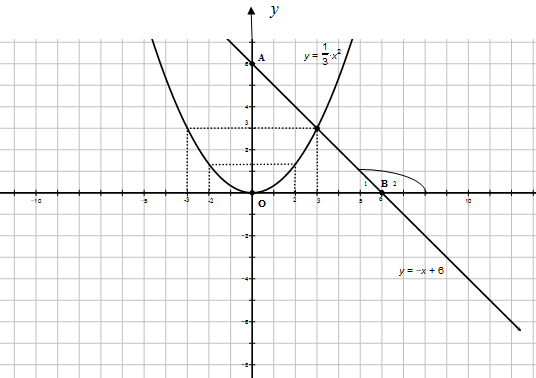
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm số đo của góc tạo bởi đường thẳng (d) và trục ox.
Đáp án đúng là: A
Quảng cáo
Bình luận về bài toán:
Câu a của bài này là một câu quen thuộc với các em. Chỉ cần học sinh lấy bảng giá trị chính xác, vẽ độ thị qua điểm đúng, và đẹp là đạt yêu cầu. Các em cũng cần lưu ý các giao điểm của đồ thị với các trục tọa đô ox, oy Câu b bài này có vẻ như hơi “lạ” với một số bạn. Lạ vì khái niệm về góc tạo bởi đường thẳng và trục ox các em ít để ý và học kỹ nên nắm không vững kiến thức. Các em không xác định được góc tạo bởi đường thẳng (d) và ox là góc nhọn hay góc tù. Nhiều em còn mặc định sai lầm “góc tạo bởi đường thẳng (d) và ox luôn là góc nhọn”. Các em cần nhớ lý thuyết về góc tạo bởi đường thẳng (d) y = ax+ b và trục ox (trục hoành)
+) Nếu hệ số góc a > 0 thì góc tạo bởi đường thẳng (d) và ox là góc nhọn.
+) Nếu hệ số góc a < 0 thì góc tạo bởi đường thẳng (d) và ox là góc tù.
Nếu điểm A (0,6) và B(6,0) các em chưa có trên bảng giá trị thì bắt buộc các em phải tìm ra.
Ví dụ như ở bài toán trên các em có thể làm thế này:
Gọi A ( 0, yA) là giao điểm của (d) và trục oy \((\Rightarrow {y_A} = - 0 + 6 \Rightarrow {y_A} = 6 \Rightarrow A\left( {0,6} \right)\)
Gọi B ( xB, 0) là giao điểm của (d) và trục ox \( \Rightarrow 0 = - {x_B} + 6 \Rightarrow {x_B} = 6 \Rightarrow B\left( {6,0} \right)\)
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
Bảng giá trị:
Đồ thị
b) Tìm số đo của góc tạo bởi đường thẳng (d) và trục ox.
Đường thẳng (d) cắt trục ox tại điểm B(6,0) và cắt trục oy tại điểm A(0,6) \( \Rightarrow OA = 6cm,OB = 6cm\)
Xét tam giác vuông AOB, ta có: \(\tan {B_1} = {{OA} \over {OB}} = {6 \over 6} = 1 \Rightarrow {\mathop B\limits^\^ _1} = {45^0})\)
Do hệ số góc a = -1 < 0 nên góc tạo bởi đường thẳng y = -x + 6 và trục Ox là góc tù
Số đo của góc tạo bởi đường thẳng (d) vả trục ox là: \({\mathop B\limits^\^ _2} = {180^0} - {\mathop B\limits^\^ _1} = {180^0} - {45^0} = {135^0}\)
Đáp án cần chọn là: A
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
