Người ta gắn một hình nón có bán kính đáy R = 8cm, độ dài đường cao h = 20 cm vào một nửa

Câu hỏi số 212570:

Vận dụng

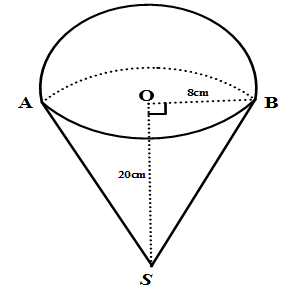
Người ta gắn một hình nón có bán kính đáy R = 8cm, độ dài đường cao h = 20 cm vào một nửa hình cầu có bán kính bằng bán kính hình nón (theo hình bên). Giá trị gần đúng thể tích của hình tạo thành (kết quả làm tròn đến chữ số thập phân thứ nhất) là :

A. \(2413\ c{m^3}\)

B. \(1413\ c{m^3}\)

C. \(2410\ c{m^3}\)

D. \(2419\ c{m^3}\)

Đáp án đúng là: A

Quảng cáo

Xem lời giải

Câu hỏi:212570

Phương pháp giải

Đây là một bài tập về hình không gian, các em sẽ được học trong chương cuối toán lớp 9. Bài toán không quá khó. Nhưng tôi chắc chắn rằng sẽ có nhiều em đọc lướt qua, thậm chí mặc định không đọc luôn vì nghĩ rằng mình sẽ không làm được bài này vì thấy cái hình trông “sợ sợ “ sao ấy. Chính cái tâm lý chưa làm đã sợ đã làm mất đi của các em 1 điểm quý giá mà không mất quá nhiều công sức ( bài giải phía dưới khá ngắn gọn). Tâm lý đó gọi là: “chưa đá đã thấy thua Thái Lan của đội bóng đá nam Việt Nam” Khi làm loại bài tập này, việc đầu tiên là các em phải phân tích xem hình đã cho được cấu tạo từ những hình nào ( trong hình vẽ ở trên là một nửa hình cầu phía trên, và một hình nón phía dưới). Sau đó, các em dùng các công thức đã biết để tính được thể tích của các hình đó. Thể tích của hình đã cho là tổng thể tích của các hình mà các em vừa tính được. Sau đây là một số công thức cho các hình các em được học trong chương trình:

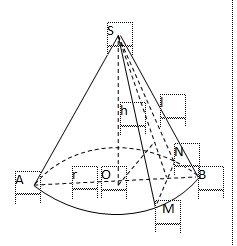
Hình nón

Diện tích xung quanh của hình nón tròn xoay: \({{S}_{xq}}=\pi rl\)

Trong đó: r là bán kính đường tròn đáy.

l là độ dày đường sinh

Thể tích của khối nón tròn xoay: \(V=\frac{1}{3}\pi {{r}^{2}}h\)

Trong đó: r là bán kính đường tròn đáy.

h là độ dày đường cao hình nón

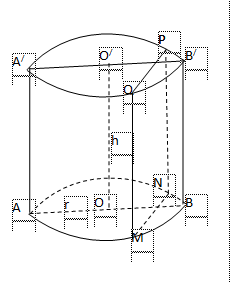
Hình trụ

Diện tích xung quanh của khối trụ tròn xoay: \({{S}_{xq}}=2\pi rh\)

Trong đó: r là bán kính đường tròn đáy.

h là độ dày đường cao hình trụ

Thể tích của khối trụ tròn xoay: \(V=\pi {{r}^{2}}h\)

Trong đó: r là bán kính đường tròn đáy.

h là độ dài đường cao hình trụ

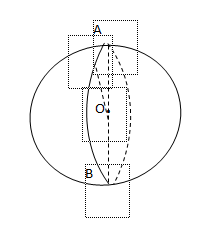
Hình cầu

Diện tích của mặt cầu: \(S=4\pi {{r}^{2}}\)

Trong đó: r là bán kính mặt cầu.

Thể tích của khối cầu: \(V=\frac{4}{3}\pi {{r}^{3}}\)

Trong đó: r là bán kính mặt cầu.

Giải chi tiết

Thể tích của một nửa hình cầu là:

\({{V}_{1}}=\frac{1}{2}.\frac{4}{3}\pi {{R}^{3}}=\frac{2}{3}\pi {{.8}^{3}}=\frac{1024}{3}\pi \left( c{{m}^{3}} \right)\)

Thể tích của hình nón là:

\({{V}_{2}}=\frac{1}{3}Sh=\frac{1}{3}.\pi {{R}^{2}}.h=\frac{1}{3}\pi {{.8}^{2}}.20=\frac{1280}{3}\pi \left( c{{m}^{3}} \right)\)

Thể tích của hình tạo thành là:

\(V={{V}_{1}}+{{V}_{2}}=\frac{1024}{3}\pi +\frac{1280}{3}\pi =768\pi =2413\left( c{{m}^{3}} \right)\)

Đáp án cần chọn là: A

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link