Cho tứ diện ABCD có các cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Cắt tứ diện bới mp(GCD)
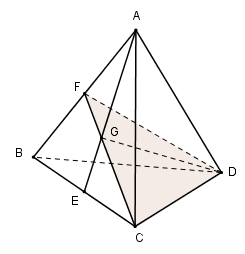
Cho tứ diện ABCD có các cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Cắt tứ diện bới mp(GCD) thì diện tích của thiết diện là:
Đáp án đúng là: B
Quảng cáo
- Dựng thiết diện của hình chóp khi cắt bởi mp(GCD).
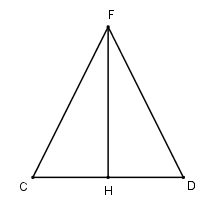
- Chứng minh thiết diện là tam giác cân. Tính diện tích tam giác cân đó bằng cách kẻ thêm đường cao.
Trong (ABC) gọi \(F=CG\cap AB\) ta có:
\(\begin{array}{l}\left( {GCD} \right) \cap \left( {ABC} \right) = CF,\\\left( {GCD} \right) \cap \left( {ABD} \right) = DF\\\left( {GCD} \right) \cap \left( {BCD} \right) = CD\end{array}\)
Vậy thiết diện là tam giác FCD.
Tam giác ABC và ABD là tam giác đều cạnh a nên \(FC=FD=\frac{a\sqrt{3}}{2}\Rightarrow \Delta FCD\)cân tại F.
Kẻ \(FH\bot CD\Rightarrow H\) là trung điểm của CD.
Xét tam giác vuông FCH có: \(FH=\sqrt{F{{C}^{2}}-C{{H}^{2}}}=\sqrt{\frac{3{{a}^{2}}}{4}-\frac{{{a}^{2}}}{4}}=\frac{a\sqrt{2}}{2}.\)
\(\Rightarrow {{S}_{FCD}}=\frac{1}{2}FH.CD=\frac{1}{2}\frac{a\sqrt{2}}{2}.a=\frac{{{a}^{2}}\sqrt{2}}{4}.\)
Đáp án cần chọn là: B
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
