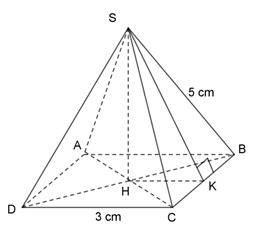
Cho hình chóp tứ giác đều S.ABCD, đáy ABCD là hình vuông có cạnh 3 cm, cạnh bên SB bằng 5 cm. a)
Cho hình chóp tứ giác đều S.ABCD, đáy ABCD là hình vuông có cạnh 3 cm, cạnh bên SB bằng 5 cm.
a) Tính đường cao SH của hình chóp.
b) Tính diện tích xung quanh và thể tích hình chóp.
Đáp án đúng là: C
Quảng cáo
- Vận dụng kiến thức đã học (định lý Pitago, đường cao, đường trung tuyến, tam giác đều, tam giác cân) và kiến thức mới (cách tính diện tích xung quanh và tính thể tích của hình chóp đều) để giải bài tập.
Lấy H là giao của 2 đường chéo hình vuông AC và BD, khi đó ta có SH là đường cao của hình chóp đều.
Kẻ SK vuông góc với BC (\(K\in BC\))
a) Áp dụng định lý Pitago cho tam giác ABC vuông tại B:
\(\begin{align} & \ \ \ \ A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} \\ & \Leftrightarrow A{{C}^{2}}={{3}^{2}}+{{3}^{2}}=18 \\ & \Rightarrow AC=\sqrt{18}=3\sqrt{2}\ cm \\ \end{align}\)
\(\Rightarrow HC=\frac{1}{2}AC=\frac{1}{2}.3\sqrt{2}=\frac{3\sqrt{2}}{2}\ cm\) (Vì H là trung điểm AC)
Áp dụng định lý Pitago cho tam giác SHC vuông tại H có:
\(\begin{align} & \ \ \ \ S{{H}^{2}}+H{{C}^{2}}=S{{C}^{2}} \\ & \Leftrightarrow S{{H}^{2}}=S{{C}^{2}}-H{{C}^{2}}={{5}^{2}}-{{\left( \frac{3\sqrt{2}}{2} \right)}^{2}}=\frac{82}{4}=\frac{41}{2} \\ & \Rightarrow SH=\frac{\sqrt{82}}{2}\ cm. \\ \end{align}\)
b) Vì tam giác SBC là tam giác cân tại S nên SK vừa là đường cao vừa là đường trung tuyến.
\(\Rightarrow CK=KB=\frac{1}{2}BC=\frac{3}{2}\ cm\)
Áp dụng định lý Pitago cho tam giác SKB vuông tại K:
\(\begin{align} & \ \ \ S{{K}^{2}}+K{{B}^{2}}=S{{B}^{2}} \\ & \Leftrightarrow S{{K}^{2}}=S{{B}^{2}}-K{{B}^{2}}={{5}^{2}}-{{\left( \frac{3}{2} \right)}^{2}}=\frac{91}{4} \\ & \Rightarrow SK=\frac{\sqrt{91}}{2}\ cm. \\ \end{align}\)
Vậy diện tích xung quanh của hình chóp đều S.ABCD là:
\({{S}_{xq}}=\frac{1}{2}.(3.4).\frac{\sqrt{91}}{2}=3\sqrt{91}\ c{{m}^{2}}\)
Vậy thể tích hình chóp đều S.ABCD là:
\(V=\frac{1}{3}.3.3.\frac{\sqrt{82}}{2}=\frac{3\sqrt{82}}{2}\ c{{m}^{3}}\)
- Học sinh cần ghi nhớ công thức tính thể tích, tính diện tích xung quanh của hình chóp đều.
- Học sinh cần xác định chính xác cạnh góc vuông, cạnh huyền của tam giác vuông để vận dụng định lý Pitago đúng.
- Học sinh cẩn thận trong tính toán đại số.
Đáp án cần chọn là: C
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
