Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm \(x \in \left[ {0;1}
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm \(x \in \left[ {0;1} \right]\).
\(2{\sin ^2}\frac{{2x}}{{1 + {x^2}}} - \sin \frac{{2x}}{{1 + {x^2}}} - m = 0\).
Đáp án đúng là: B
Quảng cáo
+) Đặt \(u = \frac{{2x}}{{1 + {x^2}}}\), tìm khoảng giá trị của u.
+) Đặt \(t = \sin u\), tìm khoảng giá trị của t.
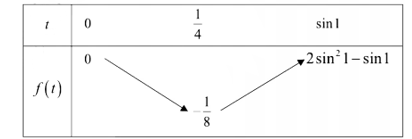
+) Đưa phương trình về dạng \(f\left( t \right) = m\). Lập BBT của hàm số \(y = f\left( t \right)\) trên khoảng giá trị của t và biện luận.
Đặt \(u = \frac{{2x}}{{1 + {x^2}}}\). \(x \in \left[ {0;1} \right] \Rightarrow u \in \left[ {0;1} \right]\). Khi đó phương trình trở thành: \(2{\sin ^2}u - \sin u - m = 0\)
Đặt \(t = \sin u;\,\,u \in \left[ {0;1} \right] \Rightarrow t \in \left[ {0;\sin 1} \right]\), phương trình trở thành \(2{t^2} - t - m = 0 \Leftrightarrow 2{t^2} - t = m\,\,\left( * \right)\) (với \(t \in \left[ {0;\sin 1} \right]\)).
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(f\left( t \right) = 2{t^2} - t\) (với \(t \in \left[ {0;\sin 1} \right]\)) và đường thẳng \(y = m\) song song với trục hoành.
Xét hàm số \(f\left( t \right) = 2{t^2} - t\) (với \(t \in \left[ {0;\sin 1} \right]\)) ta có BBT:
Khi đó phương trình (*) có nghiệm \(t \in \left[ {0;\sin 1} \right] \Leftrightarrow - \frac{1}{8} \le m \le 2{\sin ^2}1 - \sin 1\).
Đáp án cần chọn là: B
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
