Hai vật nhỏ có cùng khối lượng m = 100 g dao động điều hòa cùng tần số, chung vị trí cân

Câu hỏi số 299965:

Vận dụng cao

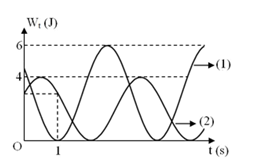
Hai vật nhỏ có cùng khối lượng m = 100 g dao động điều hòa cùng tần số, chung vị trí cân bằng trên trục Ox. Thời điểm t = 0, tỉ số li độ của hai vật là \(\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{\sqrt{6}}{2}\) . Đồ thị biểu diễn mối quan hệ giữa thế năng của hai vật theo thời gian như hình vẽ. Lấy π² = 10. Khoảng cách giữa hai chất điểm tại thời điểm t = 3,69 s gần giá trị nào sau đây nhất ?

A. 4m

B. 6m

C. 7m

D. 5m

Đáp án đúng là: D

Quảng cáo

Xem lời giải

Câu hỏi:299965

Phương pháp giải

- Công thức tính thế năng: W_t = 0,5kx²

- Công thức tính cơ năng: W = 0,5kA²

- Thế năng cực đại bằng cơ năng của vật.

- Tần số góc \(\omega =\sqrt{\frac{k}{m}}\)

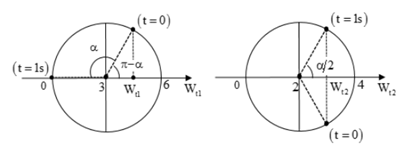
- Hai vật cùng tần số nên cùng chu kỳ dao động. Sau t = 1s góc quay được của hai dao động như nhau. Dao động 1 ở vị trí có thế năng bằng 0

Giải chi tiết

Gọi phương trình dao động của 2 vật lần lượt là:

\({{x}_{1}}={{A}_{1\,}}\cos \left( \omega t+{{\varphi }_{1}} \right)\Rightarrow W{{t}_{1}}=3\cos \left( 2\omega t+2{{\varphi }_{1}} \right)+3\)

\({{x}_{2}}={{A}_{2\,}}\cos \left( \omega t+{{\varphi }_{2}} \right)\Rightarrow {{W}_{{{t}_{2}}}}=2\cos \left( 2\omega t+2{{\varphi }_{2}} \right)+2\)

Từ t =0 đến t=1s, hai vật đều quay được cùng góc \(\alpha \) như trên đường tròn:

\({{\text{W}}_{{{t}_{1}}}}=3.\cos \left( \pi -\alpha \right)\)

\({{\text{W}}_{{{t}_{2}}}}=2.\cos \left( \pi /2 \right)\)

Vì \({{\omega }_{1}}={{\omega }_{2}},\,{{m}_{1}}={{m}_{2}}=m\Rightarrow {{k}_{1}}={{k}_{2}}=k\) và \(\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{\sqrt{6}}{2}\Rightarrow \frac{{{\text{W}}_{{{t}_{1}}}}}{{{\text{W}}_{{{t}_{2}}}}}=\frac{6}{4}\,\,\,\,\left( 2 \right)\)

Từ (1) và (2), suy ra: \(\alpha =\frac{2\pi }{3}rad\)

\(2{{\varphi }_{1}}=\frac{\pi }{3}\Rightarrow {{\varphi }_{1}}=\frac{\pi }{6}\)

\(2{{\varphi }_{2}}=-\frac{\pi }{3}\Rightarrow {{\varphi }_{2}}=-\frac{\pi }{6}\)

Từ t =0 đến t=1 s hết s

\(\Rightarrow {{\omega }_{t}}=\frac{\alpha }{1}=\frac{2\pi }{3}\Rightarrow \omega =\frac{\omega t}{2}=\frac{\pi }{3}\left( \frac{rad}{s} \right)\Rightarrow k={{\omega }^{2}}m={{\left( \frac{\pi }{3} \right)}^{2}}.0,1=\frac{1}{9}\left( \frac{N}{m} \right)\)

\({{A}_{1}}=\sqrt{\frac{2W{{t}_{1}}_{\max }}{k}}=\sqrt{\frac{2.6}{1/9}}=6\sqrt{3}m\); \({{A}_{2}}=\sqrt{\frac{2W{{t}_{2}}_{\max }}{k}}=\sqrt{\frac{2.4}{1/9}}=6\sqrt{2\,}\,m\)

Từ đó: \({{x}_{1}}=6\sqrt{3}\cos \left( \frac{\pi }{3}t+\frac{\pi }{6} \right)\,\,m\); \({{x}_{2}}=6\sqrt{2}\cos \left( \frac{\pi }{3}t-\frac{\pi }{6} \right)\,\,m\)

\(\Rightarrow d={{x}_{1}}-{{x}_{2}}=6\sqrt{3}\angle \left( \frac{\pi }{6} \right)-6\sqrt{2}\angle \left( \frac{-\pi }{6} \right)=9,58\angle 1,4\)

Hay \(d=9,58\cos \left( \frac{\pi }{3}t+1,4 \right)\,m\)

Thay \(t=3,69\,s\) vào d ta tìm được khoản cách giữa 2 vật là:

\(d=9,58cos\left( \frac{\pi }{3}.3,69+1,4 \right)\approx 5,02\,m\)

Đáp án cần chọn là: D

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.