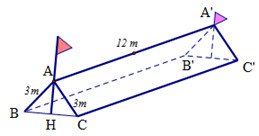
Trong một đợt tổ chức cho học sinh tham gia dã ngoại ngoài trời. Để có thể có chỗ nghỉ
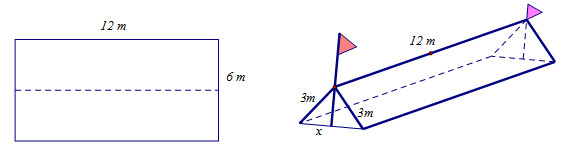
Trong một đợt tổ chức cho học sinh tham gia dã ngoại ngoài trời. Để có thể có chỗ nghỉ ngơi trong quá trình tham quan dã ngoại, các bạn học sinh đã dựng trên mặt đất bằng phẳng 1 chiếc lều bằng bạt từ một tấm bạt hình chữ nhật có chiều dài là \(12\,m\) và chiều rộng là \(6\,m\) bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm bạt sao cho hai mép chiều dài còn lại của tấm bạt sát đất và cách nhau \(x\,(m)\) (xem hình vẽ). Tìm \(x\) để khoảng không gian phía trong lều là lớn nhất?
Đáp án đúng là: B
Quảng cáo
+ Xác định rằng không gian phía trong lều chính là thể tích hình lăng trụ.
+ Tính thể tích lều theo \(x\) .
+ Tìm \(x\) để hàm số đạt giá trị lớn nhất bằng cách sử dụng bất đẳng thức \(ab \le \dfrac{{{a^2} + {b^2}}}{2}\) hoặc dùng hàm số.
Gọi tên như hình vẽ với \(AH \bot BC \Rightarrow H\) là trung điểm của \(BC \Rightarrow BH = \dfrac{{BC}}{2} = \dfrac{x}{2}\)
Xét tam giác \(AHB\) vuông tại \(B,\) theo định lý \(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{3^2} - \dfrac{{{x^2}}}{4}} = \dfrac{{\sqrt {36 - {x^2}} }}{2}\,\,\left( {0 < x < 6} \right)\)
\({V_{ABC.A'B'C'}} = {S_{ABC}}.AA' = \dfrac{1}{2}AH.BC.AA' = \dfrac{1}{2}\dfrac{{\sqrt {36 - {x^2}} }}{2}.x.12 = 3x\sqrt {36 - {x^2}} \)
Áp dụng bất đẳng thức \(ab \le \dfrac{{{a^2} + {b^2}}}{2}\) , ta có \(x\sqrt {36 - {x^2}} \le \dfrac{{{x^2} + 36 - {x^2}}}{2} \Leftrightarrow x\sqrt {36 - {x^2}} \le 18 \Leftrightarrow 3x\sqrt {36 - {x^2}} \le 54\)
Dấu “=” xảy ra khi \(x = \sqrt {36 - {x^2}} \Leftrightarrow 2{x^2} = 36 \Leftrightarrow \left[ \begin{array}{l}x = - 3\sqrt 2 \,\left( {ktm} \right)\\x = 3\sqrt 2 \,\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy \({V_{\max }} = 54 \Leftrightarrow x = 3\sqrt 2 .\)
Các em có thể sử dụng hàm số như sau
\(V' = 3\sqrt {36 - {x^2}} + 3x.\dfrac{{ - 2x}}{{2\sqrt {36 - {x^2}} }} = 3\sqrt {36 - {x^2}} - \dfrac{{3{x^2}}}{{\sqrt {36 - {x^2}} }}\)
\(V' = 0 \Leftrightarrow 36 - {x^2} - {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\sqrt 2 \,\,\,\,\,\,\,\left( {tm} \right)\\x = - 3\sqrt 2 \,\,\,\left( {ktm} \right)\end{array} \right.\)
Bảng xét dấu
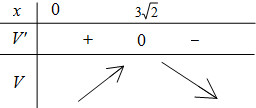
\( \Rightarrow {V_{\max }} = V\left( {3\sqrt 2 } \right)\)
Đáp án cần chọn là: B
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
