Cho \(\Delta ABC\) cân tại \(A\,\left( {\angle A < {{90}^0}} \right)\) ; Các đường cao \(BD;CE\left( {D \in

Câu hỏi số 311623:

Vận dụng

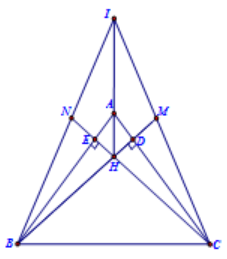
Cho \(\Delta ABC\) cân tại \(A\,\left( {\angle A < {{90}^0}} \right)\) ; Các đường cao \(BD;CE\left( {D \in AC;E \in AB} \right)\)cắt nhau tại \(H.\)

a) Chứng minh : \(\Delta ABD = \Delta ACE.\)

b) \(\Delta BHC\) là tam giác gì ? Vì sao ?

c) So sánh đoạn \(HB\) và \(HD?\)

d) Trên tia đối của tia \(EH\) lấy điểm \(N\) sao cho \(NH < HC;\) Trên tia đối của tia \(DH\) lấy điểm \(M\) sao cho \(MH = NH.\) Chứng minh các đường thẳng \(BN;AH;CM\) đồng quy.

Quảng cáo

Xem lời giải

Câu hỏi:311623

Phương pháp giải

a) Chứng minh hai tam giác vuông bằng nhau theo trường hợp: cạnh huyền – góc nhọn.

b) Chỉ ra \(\Delta BHC\) là tam giác cân với hai góc ở đáy bằng nhau.

c) Dựa vào mối liên hệ giữa các đường trong tam giác để so sánh các đoạn thẳng: HB và HD.

d) Các đường đồng quy trong tam giác, dựa vào các tính chất và dấu hiệu đã học để chứng minh.

Giải chi tiết

a) Xét \(\Delta ABD\& \Delta ACE\) có: \(\angle ADB = \angle ACE = {90^0}\left( {gt} \right)\)

\(\begin{array}{l}BA = AC\left( {gt} \right)\\\angle BAC\,\,\,chung\end{array}\)

\( \Rightarrow \Delta ABD = \Delta ACE\) (cạnh huyền – góc nhọn)

b) Có \(\Delta ABD = \Delta ACE \Rightarrow \angle ABD = \angle ACE\) (hai góc tương ứng)

Mặt khác: \(\angle ABC = \angle ACB\) (\(\Delta ABC\) cân tại A)

\(\begin{array}{l} \Rightarrow \angle ABC - \angle ABD = \angle ACB - \angle ACE\\ \Rightarrow \angle HBC = \angle HCB\end{array}\)

\( \Rightarrow \Delta BHC\) là tam giác cân tại H

c) Có \(\Delta HDC\) vuông tại \(D\) nên \(HD < HC\)

mà \(HB = HC\) (\(\Delta BHC\) cân tại H)

\( \Rightarrow HD < HB\)

d) Gọi \(I\) là giao điểm của \(BN\) và \(CM\)

Xét \(\Delta BNH\) và \(\Delta CMH\) có :

\(BH = CH\,\)(\(\Delta BHC\) cân tại H)

\(\angle BH{\rm N} = \angle CHM\) (đối đỉnh)

\({\rm N}H = HM\left( {gt} \right)\)

\( \Rightarrow \Delta B{\rm N}H = \Delta CMH\left( {c.g.c} \right) \Rightarrow \angle HB{\rm N} = \angle HCM\)

+) Lại có : \(\angle HBC = \angle HCB\,\,\left( {cmt} \right)\)

\( \Rightarrow \angle HBC + \angle HB{\rm N} = \angle HCB + \angle HCM \Rightarrow \angle IBC = \angle ICB\)

\( \Rightarrow \Delta IBC\) cân tại \(I \Rightarrow IB = IC\,\,\,\,\left( 1 \right)\)

Mặt khác ta có : \(AB = AC\,\) (\(\Delta ABC\) cân tại A). (2)

\(HB = HC\) (\(\Delta BHC\) cân tại H) (3)

Từ (1), (2), (3)

\( \Rightarrow \) 3 điểm \(I;A;H\) cùng nằm trên đường trung trực của \(BC\)

\( \Rightarrow I;A;H\) thẳng hàng

\( \Rightarrow \) các đường thẳng \(B{\rm N};AH;CM\) đồng quy.

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link