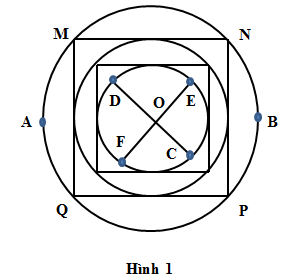
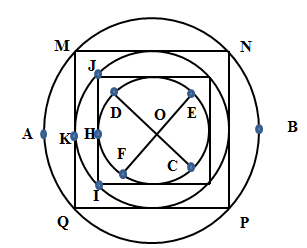
Hệ thống đường đi trong một công viên trò chơi tìm mật thư được thiết kế gồm: ba đường
Hệ thống đường đi trong một công viên trò chơi tìm mật thư được thiết kế gồm: ba đường tròn đồng tâm O, hai hình vuông, hai đoạn thẳng CD và EF. Các đường tròn và hình vuông lần lượt ngoại, nội tiếp nhau (Hình 1). Đường tròn lớn nhất có đường kính D1 = 100m, đường tròn trong cùng chứa các điểm C, E, D, F lần lượt là trung điểm của các cung giới hạn giữa hai tiếp điểm liền kề. Những đường đi hình tròn (hoặc cung tròn) được trải sỏi, những đường đi hình vuông (hoặc đường đi thẳng) được lát bê tông. Mật thư được đặt tại tâm O, người chơi xuất phát từ một trong hai cửa vào A hoặc vào B (AB là đường kính đường tròn lớn, song song với hai trong các cạnh của mỗi hình vuông) trên đường tròn ngoài cùng. Sau khi lấy được mật thư, người chơi phải đi ra bằng một đường khác so với lúc đi vào để gặp ban tổ chức tại một trong bốn trạm M, N, P, Q ở bốn đỉnh của hình vuông lớn.
a) Một học sinh có tốc độ chạy trên đường trải sỏi là 5km/h, chạy trên đường bê tông là 7,5km/h tham gia trò chơi. Hãy chỉ ra đường đi với thời gian ngắn nhất giúp học sinh này (bằng cách đặt tên cho các đoạn đường) để lấy được mật thư và tính thời gian đi hết đoạn đường đó.
b) Sau khi lấy được mật thư, học sinh đó phải đi ra bằng đường khác lúc đi vào mới hợp lệ. Giả sử học sinh tìm được đường ra cũng ngắn nhất. Hỏi thời gian đi ra dài hơn hay ngắn hơn thời gian đi vào? Tính khoảng thời gian chênh lệch đó?
Coi bề rộng mỗi cung đường không đáng kể so với chiều dài của nó; bỏ qua thời gian di chuyển khi chạy qua phần tiếp xúc giữa hai cung đường.
Quảng cáo
Đổi đơn vị: \(\left\{ \begin{array}{l}5km/h = \frac{{25}}{{16}}m/s\\7,5km/h = \frac{{25}}{{12}}m/s\end{array} \right.\)
Đường đi từ A → M → I → H → D → O
Đường về: O → F → H → I → K → Q
K là tiếp điểm của MQ với đường tròn ở giữa
I, J là hai đỉnh của hình vuông thứ 2
H là tiếp điểm của IJ với đường tròn trong cùng.
Vậy đường ra và đường vào là như nhau → Chênh lệch thời gian bằng 0
a)
Đường kính của đường tròn (2) bằng độ dài một dây cung MQ của đường tròn (1)
Ta có: \({D_2} = MQ = \frac{{{D_1}}}{{\sqrt 2 }} = 50\sqrt 2 m\)
Tương tự: \({D_3} = IJ = \frac{{{D_2}}}{{\sqrt 2 }} = \frac{{{D_1}}}{2} = 50m\)
*) Các đoạn đường sỏi phải đi là các cung: cung AM, cung AJ, cung HD
\(\eqalign{
& cung\,AM = {1 \over 8}{P_1} = {1 \over 8}\pi {D_1} \cr
& cung\,KI = {1 \over 8}{P_2} = {1 \over 8}\pi {D_2} = {1 \over 8}\pi .{{{D_1}} \over {\sqrt 2 }} \cr
& cung\,HD = {1 \over 8}{P_3} = {1 \over 8}\pi {D_3} = {1 \over {16}}\pi {D_1} \cr} \)
*) Các đoạn đường bê tông phải đi là:
\(\begin{array}{l}MK = \frac{1}{2}MQ = \frac{1}{2}{D_2} = 25\sqrt 2 m\\HD = \frac{1}{2}IJ = \frac{1}{2}{D_3} = 25m\\OD = \frac{1}{2}{D_3} = 25m\end{array}\)
*) Tổng thời gian phải di chuyển là:
\(t = {{cung\,AM + cung\,KI + cung\,HD} \over {{{25} \over {18}}}} + {{MK + HD + OD} \over {{{25} \over {12}}}} = 62,37 + 40,97 = 103,34\)
b)
Đường đi từ A → M → I → H → D → O
Đường về: O → F → H → I → K → Q
K là tiếp điểm của MQ với đường tròn ở giữa
I, J là hai đỉnh của hình vuông thứ 2
H là tiếp điểm của IJ với đường tròn trong cùng.
Vậy đường ra và đường vào là như nhau → Chênh lệch thời gian bằng 0
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
