Một miếng gỗ mỏng hình tròn, bán kính \(4cm\). Người ta cắm thẳng góc một chiếc đinh qua tâm
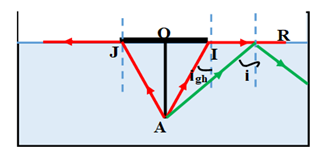
Một miếng gỗ mỏng hình tròn, bán kính \(4cm\). Người ta cắm thẳng góc một chiếc đinh qua tâm O của miếng gỗ nổi trong chậu nước. Thành chậu thẳng đứng và rìa miếng gỗ cách thành chậu \(10cm\). Nước có chiết suất \(n=1,33\). Gọi chiều dài phần đinh nằm trong nước là \(OA=6cm\). Tìm chiều dài lớn nhất của OA sao cho dù để mắt ở đâu cũng không thấy đầu A của đinh.
Đáp án đúng là: C
Quảng cáo
+ Định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}\sin r\)
+ Điều kiện để có phản xạ toàn phần: \(\left\{ \begin{array}{l}{n_2} < {n_1}\\i \ge {i_{gh}};\,\,\left( {\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}}} \right)\end{array} \right.\)
Một miếng gỗ mỏng hình tròn, bán kính; R = 4cm
Điều kiện để mắt ở đâu cũng không thấy đầu A của đinh là: Tia sáng từ A phát ra truyền tới mặt nước thì không cho tia khúc xạ ra ngoài không khí.
Ta thấy góc tới i của tia sáng phát ra từ A đến mặt nước tăng dần khi vị trí tới di chuyển từ điểm I của mép miếng gỗ ra xa tâm O. Để không có bất kỳ tia khúc xạ nào lọt ra ngoài không khí thì tia tới AI phải có góc tới thỏa mãn điều kiện:
\(i{\rm{ }} \ge {i_{gh}}\; \Leftrightarrow \sin i \ge \sin {i_{gh}}\; = \dfrac{1}{n}\)
Ta có: \({\sin i = \sin \widehat {OAI} = \frac{{OI}}{{AI}} = \frac{R}{{\sqrt {O{A^2} + {R^2}} }} \ge \frac{1}{n}}\)
\({ \Leftrightarrow \sqrt {O{A^2} + {R^2}} \le R.n \Leftrightarrow O{A^2} + {R^2} \le {R^2}.{n^2}}\)
\({ \Leftrightarrow OA \le R\sqrt {{n^2} - 1} = 4.\sqrt {1,{{33}^2} - 1} = 3,51cm}\)
\({ \Rightarrow O{A_{\max }} = 3,51cm}\)
Đáp án cần chọn là: C
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
