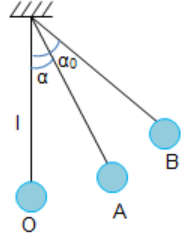
Một con lắc đơn có chiều dài \(0,8m\). Kéo lệch dây treo con lắc hợp với phương thẳng đứng
Một con lắc đơn có chiều dài \(0,8m\). Kéo lệch dây treo con lắc hợp với phương thẳng đứng góc \({60^0}\) rồi thả nhẹ. Bỏ qua lực cản không khí. Lấy \(g = 10{\rm{ }}m/{s^2}\). Chọn gốc thế năng tại vị trí thấp nhất của vật. Tính tốc độ cực đại của con lắc đạt được trong quá trình dao động.
Đáp án đúng là: A
Quảng cáo
Áp dụng định luật bảo toàn cơ năng.
Cơ năng của vật chuyển động trong trọng trường:\({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t}\)
Chọn gốc thế năng tại O.
+ Cơ năng của vật tại O:
\({{\rm{W}}_O} = {{\rm{W}}_{tO}} + {{\rm{W}}_{dO}} = \dfrac{1}{2}mv_{\max }^2\)
+ Cơ năng của vật tại B:
\({{\rm{W}}_B} = {{\rm{W}}_{tB}} + {{\rm{W}}_{dB}} = mg.{z_B} = mg.l.\left( {1 - \cos {\alpha _0}} \right)\)
Áp dụng định luật bảo toàn cơ năng tại O và B ta có:
\(\begin{array}{*{20}{l}}
{{{\rm{W}}_O} = {{\rm{W}}_B} \Leftrightarrow \frac{1}{2}m{v_{{{\max }^2}}} = mgl.\left( {1 - \cos {\alpha _0}} \right)}\\
\begin{array}{l}
\Rightarrow {v_{\max }} = \sqrt {2gl.\left( {1 - \cos {\alpha _0}} \right)} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {2.10.0,8.\left( {1 - \cos 60} \right)} = 2\sqrt 2 m/s
\end{array}
\end{array}\)
Đáp án cần chọn là: A
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
