Ca-bin thang máy tòa nhà A của Trường Phổ thông Năng khiếu đi từ tầng 1 lên tầng 8 hết 25 s,

Câu hỏi số 406353:

Vận dụng cao

Ca-bin thang máy tòa nhà A của Trường Phổ thông Năng khiếu đi từ tầng 1 lên tầng 8 hết 25 s, từ tầng 1 lên tầng 7 hết \(21\dfrac{2}{3}\,\,\,s\) (hai tầng liên tiếp cách nhau 4,5 m). Mỗi lần xuất phát cho đến khi dừng lại (đi lên cũng như đi xuống) đồ thị tốc độ v của ca-bin (CB) theo thời gian t luôn là một hình thang cân như Hình 1. (Chiều dài đoạn KL tùy thuộc quãng đường di chuyển; v₁, t₁ là những hằng số chưa biết, có giá trị như nhau đối với mọi quá trình chuyển động của thang máy.

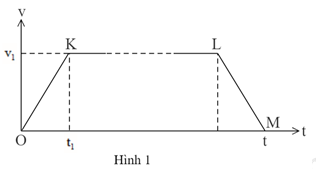
a. Tính tốc độ trung bình của CB khi đi từ tầng 1 lên tầng 8

b. Chứng minh rằng quãng đường CB đi được trong thời gian t tính từ lúc xuất phát, bằng diện tích hình thang OKLM.

c. Tính thời gian khi CB chỉ đi từ tầng 7 lên tầng 8; từ tầng 3 xuống tầng 1.

Quảng cáo

Xem lời giải

Câu hỏi:406353

Phương pháp giải

Tốc độ trung bình: \({v_{tb}} = \dfrac{S}{t}\)

Quãng đường: \(S = vt\)

Giải chi tiết

a. Khoảng cách mỗi tầng là: \(L = 4,5\,\,\left( m \right)\)

Thang máy đi từ tầng 1 lên tầng 8, quãng đường CB đi được qua 7 tầng:

\(S = 7L = 7,4,5 = 31,5\,\,\left( m \right)\)

Tốc độ trung bình của thang máy khi đi từ tầng 1 lên tầng 8 là:

\({v_{tb}} = \dfrac{S}{t} = \dfrac{{31,5}}{{25}} = 1,26\,\,\left( {m/s} \right)\)

b. Ta thấy trong khoảng thời gian t₁, vận tốc tăng đều từ 0 lên v₁, do đó tốc độ trung bình của thang máy trong khoảng thời gian này là: \({v_{tb1}} = \dfrac{{{v_1}}}{2}\)

Quãng đường thang máy đi được trong thời gian t là:

\(\begin{array}{l}S = 2{v_{tb1}}.{t_1} + {v_1}.\left( {t - 2{t_1}} \right) = 2\dfrac{{{v_1}}}{2}{t_1} + {v_1}.\left( {t - 2{t_1}} \right)\\ \Rightarrow S = {v_1}{t_1} + {v_1}.\left( {t - 2{t_1}} \right) = {v_1}t - {v_1}{t_1}\\ \Rightarrow S = \dfrac{{{v_1}}}{2}.\left( {2t - 2{t_1}} \right) = \dfrac{{{v_1}}}{2}.\left[ {t + \left( {t - 2{t_1}} \right)} \right]\end{array}\)

Mà \({S_{OKLM}} = \dfrac{{t + \left( {t - 2{t_1}} \right).{v_1}}}{2} = \dfrac{{{v_1}}}{2}.\left[ {t + \left( {t - 2{t_1}} \right)} \right]\)

Vậy S = S_OKLM (đpcm)

c. Độ chệnh lệch thời gian khi thang máy đi từ tầng 1 lên tầng 8 và từ tầng 1 lên tầng 7 là:

\(\Delta t = {t_8} - {t_7} = 25 - 21\dfrac{2}{3} = \dfrac{{10}}{3}\,\,\left( s \right)\)

Vậy số tầng thang máy đi được giảm đi n tầng, thời gian thang đi giảm: \(n.\Delta t\,\,\left( s \right)\)

Thời gian thang máy đi từ tầng 7 lên tầng 8, đi qua 1 tầng là:

\({t_{78}} = {t_8} - 6\Delta t = 25 - 6.\dfrac{{10}}{3} = 5\,\,\left( s \right)\)

Thời gian thang máy đi từ tầng 3 xuống tầng 1, đi qua 2 tầng là:

\({t_{31}} = {t_{78}} + \Delta t = 5 + \dfrac{{10}}{3} = 8\dfrac{1}{3}\,\,\left( s \right)\)

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link