Một con lắc lò xo treo thẳng đứng gồm vật nặng khối lượng m = 120g được tích điện \(q =
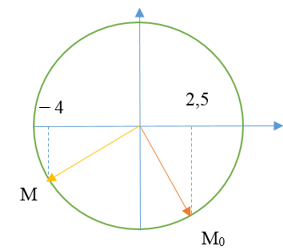
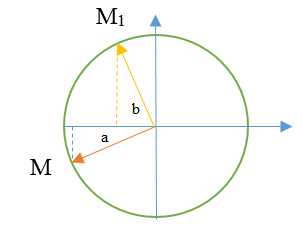
Một con lắc lò xo treo thẳng đứng gồm vật nặng khối lượng m = 120g được tích điện \(q = 2,{16.10^{ - 4}}C\). Lò xo không dẫn điện, vật cô lập về điện. Chọn gốc O tại vị trí cân bằng của vật, trục Ox thẳng đứng hướng lên. Cho vật dao động điều hòa với phương trình \(x = 5.\cos \left( {4\pi t - \frac{\pi }{3}} \right)cm\). Lấy g = 10 m/s2, π2 = 10. Ngay khi vật đi hết quãng đường 173,5 cm tính từ thời điểm t = 0, người ta thiết lập một điện trường đều có vectơ cường độ điện trường \(\overrightarrow E \) thẳng đứng hướng xuống, E = 2.103 V/m trong thời gian 1,375s rồi ngắt điện trường. Biên độ dao động của vật sau khi ngắt điện trường gần đúng bằng.
Đáp án đúng là: D
Quảng cáo
Áp dụng VTLG và công thức độc lập với thời gian:
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)
Khi áp điện trường vào thì lò xo dãn thêm một đoạn:
\(q.E = k.\Delta l \Rightarrow \Delta l = \frac{{q.E}}{k} = \frac{{q.E}}{{m.{\omega ^2}}}\)
Vị trí cân bằng của lò xo lệch đi một đoạn \(\Delta l\) , xác định tọa độ và vận tốc của vật ở đó để xác định biên độ dao động mới.
Khi ngắt điện trường, vị trí cân bằng trở về vị trí ban đầu, tại thời điểm ngắt điện trường, xác định tọa độ và vận tốc của vật ở vị trí đó để xác định biên độ dao động mới.
Vật dao động điều hòa với phương trình:\(x = 5.\cos \left( {4\pi t - \frac{\pi }{3}} \right)cm\),
\(\Rightarrow \left\{ \begin{array}{l}
A = 5cm\\
\omega = 4\pi \left( {rad/s} \right) \Rightarrow T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,5s
\end{array} \right.\)
Ban đầu vật ở vị trí có lí độ x = 2,5cm đang chuyển động theo chiều dương.
Khi vật đi quãng đường:
\(173,5cm = 2,5 + 17.10 + 1\)
VTLG cho ta vị trí ban đầu và vị trí t.
Tại M thì vận đang có vận tốc là:
\(v = \sqrt {{\omega ^2}.({A^2} - {x^2})} = \sqrt {{{(4\pi )}^2}.({5^2} - {4^2})} = 12{\pi _{}}\left( {cm/s} \right)\)
Tại vị trí này, thiết lập điện trường. Lực điện trường làm lò xo dãn thêm một đoạn ∆l :
\(qE = k.\Delta l \Rightarrow \Delta l = \frac{{qE}}{k} = \frac{{2,{{16.10}^{ - 4}}{{.2.10}^3}}}{{0,12.{{(4\pi )}^2}}} = 2,{25.10^{ - 2}}m = 2,25cm\)
Vậy vị trí cân bằng lùi xuống dưới một đoạn 2,25 cm. Khi đó vật đang có li độ:
\(x = - 4 + 2,25 = - 1,75{\rm{ }}cm\)
Thời gian thiết lập điện trường là:
\(1,375s = \frac{{11}}{4}T = 2T + \frac{3}{4}T\)
Ta có VTLG:
Ta thấy hai thời điểm vuông pha, ta có:
\(\left\{ \begin{array}{l}
x = \frac{{{v_1}}}{\omega } \Rightarrow {v_1} = \omega .x = 4\pi .\left( { - 1,75} \right) = - 7\pi \,\,\left( {cm/s} \right)\\
{x_1} = \frac{-v}{\omega } = \frac{{-12\pi }}{{4\pi }} = -3\,\,\left( {cm} \right)
\end{array} \right.\)
Lúc này ngừng tác dụng lực điện, vị trí cân bằng của vật trở về vị trí ban đầu, nên li độ của vật lúc này là:
\(x' = -3-2,25 = -5,25cm\)
Biên độ của vật là:
\(A'' = {\rm{ }}\sqrt {x{'^2} + \frac{{{v_1}^2}}{{{\omega ^2}}}} = \sqrt {{{\left( { - 5,25} \right)}^2} + {{\left( {\frac{{7\pi }}{{4\pi }}} \right)}^2}} = 5,534cm\)
Vậy gần nhất với giá trị biên độ này là 5,26 cm.
Đáp án cần chọn là: D
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
