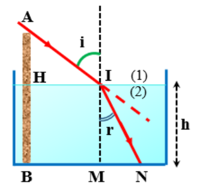
Đặt một thước dài \(70\,\,cm\) theo phương thẳng đứng vuông góc với đáy bể nước nằm ngang
Đặt một thước dài \(70\,\,cm\) theo phương thẳng đứng vuông góc với đáy bể nước nằm ngang (đầu thước chạm đáy bể). Chiều cao lớp nước là \(40\,\,cm\) và chiết suất là \(\frac{4}{3}\). Nếu các tia sáng mặt trời tới nước dưới góc tới \(i\,\,\left( {sin{\rm{ }}i = 0,8} \right)\) thì bóng của thước dưới đáy bể là
Đáp án đúng là: C
Quảng cáo
Công thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}\sin r\)
Ta có hình vẽ:
Bóng của thước dưới đáy bể bằng độ dài đoạn \(BN\)
Áp dụng công thức định luật khúc xạ ánh sáng, ta có:
\({n_1}\sin i = {n_2}\sin r \Rightarrow 1.0,8 = \frac{4}{3}.sinr \Rightarrow sinr = 0,6\)
Lại có: \(\sin r = \frac{{MN}}{{IN}} = \frac{{MN}}{{\sqrt {M{N^2} + I{M^2}} }} \Rightarrow 0,6 = \frac{{MN}}{{\sqrt {M{N^2} + {{40}^2}} }}\)
\( \Rightarrow 0,36 = \frac{{M{N^2}}}{{M{N^2} + {{40}^2}}} \Rightarrow MN = 30\,\,\left( {cm} \right)\)
Ta có: \(\sin i = \sin \widehat {HAI} = \frac{{IH}}{{AI}} \Rightarrow 0,8 = \frac{{IH}}{{\sqrt {I{H^2} + A{H^2}} }}\)
\( \Rightarrow 0,64 = \frac{{I{H^2}}}{{I{H^2} + {{30}^2}}} \Rightarrow IH = 40\,\,\left( {cm} \right)\)
Chiều dài bóng của thước dưới đáy bể là:
\(BN = BM + MN = IH + MN = 40 + 30 = 70\,\,\left( {cm} \right)\)
Đáp án cần chọn là: C
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
