Hai thấu kính, một hội tụ \(\left( {{f_1} = 20cm} \right)\), một phân kì \(\left( {{f_2} = 10cm}
Hai thấu kính, một hội tụ \(\left( {{f_1} = 20cm} \right)\), một phân kì \(\left( {{f_2} = 10cm} \right)\), có cùng trục chính. Khoảng cách hai quang tâm là \(l = 30cm\). Vật AB vuông góc với trục chính được đăt bên trái \({L_1}\) và cách \({L_1}\) một đoạn \({d_1}\). Cho \({d_1} = 20cm\), hãy tính số phóng đại ảnh cuối cùng cho bởi hệ hai thấu kính?
Đáp án đúng là: D
Quảng cáo
Sơ đồ tạo ảnh : \(AB \to {A_1}{B_1} \to {A_2}{B_2}\)
Áp dụng công thức thấu kính cho từng thấu kính : \(\left\{ \begin{array}{l}\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\\k = \frac{{\overline {A'B'} }}{{\overline {AB} }} = - \frac{{d'}}{d}\end{array} \right.\)
Chú ý : \({d_1}{\rm{' + }}{d_2} = {O_1}{O_2}\)
Hệ số phóng đại: \(k = {k_1}{k_2} = \frac{{{d_1}'}}{{{d_1}}}.\frac{{{d_2}'}}{{{d_2}}}\)
Đáp án cần chọn là: D
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com



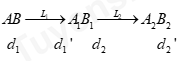

 \(\frac{1}{{{d_2}}} + \frac{1}{{{d_2}'}} = \frac{1}{{{f_2}}} \Rightarrow \frac{1}{{ - \infty }} + \frac{1}{{{d_2}'}} = \frac{1}{{{f_2}}} \Rightarrow {d_2}' = {f_2} = - 10cm\)
\(\frac{1}{{{d_2}}} + \frac{1}{{{d_2}'}} = \frac{1}{{{f_2}}} \Rightarrow \frac{1}{{ - \infty }} + \frac{1}{{{d_2}'}} = \frac{1}{{{f_2}}} \Rightarrow {d_2}' = {f_2} = - 10cm\) 







